2023-2024學年湖北省武漢市武鋼三中高三（上）月考數(shù)學試卷（10月份）

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知集合A={x|x＞-2}，B={x|x²+2x-8≥0}，則下列結(jié)論中正確的是（　　）

  A．A?B	B．A∩B=?
  C．?RA??RB	D．（?RA）∩（?RB）≠?
  組卷：30引用：3難度：0.8

  解析

• 2．某企業(yè)為了解員工身體健康情況，采用分層隨機抽樣的方法從該企業(yè)的營銷部門和研發(fā)部門抽取部分員工體檢．已知該企業(yè)營銷部門和研發(fā)部門的員工人數(shù)之比是5：1，且被抽到參加體檢的員工中，營銷部門的人數(shù)比研發(fā)部門的人數(shù)多72，則參加體檢的人數(shù)是（　　）

  A．90

  B．96

  C．108

  D．144
  組卷：53引用：1難度：0.7

  解析

• 3．已知復數(shù)

  z

  1

  =

  1

  +

  2

  i

  ,

  z

  2

  =

  3

  +

  i

  1

  +

  i

  ，

  z

  3

  =

  -

  1

  -

  2

  i

  在復平面上對應的點是一個正方形的3個頂點，則這個正方形的第4個頂點所對應的復數(shù)z₄=（　　）

  A．2-i

  B．-2+i

  C．2+i

  D．-2-i
  組卷：51引用：3難度：0.8

  解析

• 4．已知點P在棱長為2的正方體表面上運動，AB是該正方體外接球的一條直徑，則

  PA

  ?

  PB

  的最小值為（　　）

  A．-2

  B．-3

  C．-1

  D．0
  組卷：667引用：5難度：0.5

  解析

• 5．李明開發(fā)的小程序經(jīng)過t天后，用戶人數(shù)A（t）=500e^kt，其中k為常數(shù)．已知小程序發(fā)布經(jīng)過10天后有2000名用戶，則用戶超過50000名至少經(jīng)過的天數(shù)為（　　）（取lg2=0.30）

  A．31

  B．32

  C．33

  D．34
  組卷：318引用：7難度：0.6

  解析

• 6．設函數(shù)f（x）=xsinx,若

  x

  1

  ，

  x

  2

  ∈

  [

  -

  π

  2

  ，

  π

  2

  ]

  ，且f（x₁）＞f（x₂），則下列必定成立的是（　　）

  A． x 1 2 ＞ x 2 2

  B．x1＜x2

  C．x1＞x2

  D．x1+x2＞0
  組卷：199引用：3難度：0.7

  解析

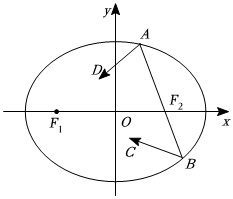• 7．古希臘數(shù)學家阿波羅尼奧斯在研究圓錐曲線時發(fā)現(xiàn)了橢圓的光學性質(zhì)：從橢圓的一個焦點射出的光線，經(jīng)橢圓反射，其反射光線必經(jīng)過橢圓的另一焦點．設橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右焦點分別為F₁，F(xiàn)₂，若從橢圓右焦點F₂發(fā)出的光線經(jīng)過橢圓上的點A和點B反射后，滿足AB⊥AD，且cos∠ABC=

  3

  5

  ，則該橢圓的離心率為（　　）

  A． 1 2

  B． 2 2

  C． 3 2

  D． 5 3
  組卷：716引用：13難度：0.6

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 21．已知A、B、C是直線l上的三點，且|AB|=1，|BC|=2，⊙O切直線l于點A，又過B、C作⊙O異于l的兩切線，設這兩切線交于點P．
  （1）求點P的軌跡E方程．
  （2）設M，N是P的軌跡E上的不同兩點且不關(guān)于原點O對稱，若OM，ON的斜率分別為k₁，k₂，問：是否存在實數(shù)λ，使得當k₁k₂=λ時，△OMN的面積是定值？如果存在，求出λ的值；如果不存在，說明理由．
  組卷：21引用：1難度：0.2

  解析

• 22．已知函數(shù)f（x）=e^ax-2ax（a∈R，a≠0）．
  （1）討論f（x）的單調(diào)性；
  （2）若不等式f（x）≥sinx-cosx+2-2ax對任意x≥0恒成立，求實數(shù)a的取值范圍．
  組卷：70引用：2難度：0.5

  解析