2022-2023學(xué)年廣東省佛山市南海一中高一（下）段考數(shù)學(xué)試卷（三）

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個(gè)選項(xiàng)中，只有一個(gè)選項(xiàng)是符合題目要求的．

• 1．若復(fù)數(shù)

  z

  =

  1

  +

  2

  i

  i

  （i為虛數(shù)單位），則|z|=（　　）

  A．1

  B．2

  C． 3

  D． 5
  組卷：72引用：5難度：0.8

  解析

• 2．△ABC的內(nèi)角A，B，C的對(duì)邊分別為a,b,c,若

  A

  =

  30

  °

  ，

  B

  =

  45

  °

  ，

  a

  =

  2

  ，則b=（　　）

  A． 6

  B．2

  C． 3

  D． 2 6
  組卷：223引用：4難度：0.8

  解析

• 3．要得到函數(shù)

  f

  （

  x

  ）

  =

  sin

  （

  2

  x

  -

  π

  6

  ）

  的圖象，只需將函數(shù)g（x）=sin2x的圖象（　　）

  A．向右平移 π 12 個(gè)單位長(zhǎng)度

  B．向右平移 π 3 個(gè)單位長(zhǎng)度

  C．向左平移 π 12 個(gè)單位長(zhǎng)度

  D．向左平移 π 3 個(gè)單位長(zhǎng)度
  組卷：147引用：4難度：0.7

  解析

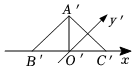• 4．用斜二測(cè)畫(huà)法畫(huà)水平放置的△ABC的直觀圖，得到如圖所示的等腰直角三角形A′B′C′．已知點(diǎn)O′是斜邊B′C′的中點(diǎn)，且O′A′=2，則△ABC的面積為（　　）

  A．4 2

  B．8 2

  C．2 2

  D．6 2
  組卷：330引用：13難度：0.7

  解析

• 5．設(shè)α，β為兩個(gè)不同的平面，m,n為兩條不同的直線(xiàn)，下列命題正確的是（　　）

  A．若m∥n,n?α，則m∥α

  B．若m∥α，n∥β，m∥n,則α∥β

  C．若m⊥β，n∥β，則m⊥n

  D．若α⊥β，α∩β=m,n⊥m,則n⊥α
  組卷：248引用：12難度：0.6

  解析

• 6．中國(guó)南北朝時(shí)期數(shù)學(xué)家、天文學(xué)家祖沖之、祖暅父子總結(jié)了魏晉時(shí)期著名數(shù)學(xué)家劉徽的有關(guān)工作，提出“冪勢(shì)既同，則積不容異”．“冪”是截面積，“勢(shì)”是幾何體的高．詳細(xì)點(diǎn)說(shuō)就是，界于兩個(gè)平行平面之間的兩個(gè)幾何體，被任一平行于這兩個(gè)平面的平面所截，如果兩個(gè)截面的面積相等，則這兩個(gè)幾何體的體積相等．上述原理在中國(guó)被稱(chēng)為祖暅原理．一個(gè)上底面邊長(zhǎng)為1，下底面邊長(zhǎng)為2高為2

  3

  的正六棱臺(tái)與一個(gè)不規(guī)則幾何體滿(mǎn)足“冪勢(shì)既同”，則該不規(guī)則幾何體的體積為（　　）

  A．16

  B．16 3

  C．18 3

  D．21
  組卷：559引用：12難度：0.7

  解析

• 7．設(shè)平面向量

  a

  ，

  b

  滿(mǎn)足

  |

  a

  |

  =

  12

  ，

  b

  =

  （

  2

  ，

  5

  ）

  ，

  a

  ?

  b

  =

  18

  ，則

  b

  在

  a

  上投影向量的模為（　　）

  A． 3 2

  B． 2 3 2

  C．3

  D．6
  組卷：389引用：4難度：0.8

  解析

四、解答題：本題共6小題，共70分．解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟．

• 21．已知向量

  m

  =

  （

  cos

  A

  ，

  sin

  B

  ）

  ，

  n

  =

  （

  cos

  B

  ，-

  sin

  A

  ）

  ，

  m

  ?

  n

  =

  cos

  2

  C

  ，其中A，B，C為△ABC的內(nèi)角，a,b,c為角A，B，C的對(duì)邊．
  （1）求C；
  （2）若2c=a+b,且abcosC=18，求c.
  組卷：656引用：3難度：0.8

  解析

• 22．如圖，四棱錐P-ABCD中，AB∥CD，∠BAD=90°，PA=AD=AB=

  1

  2

  CD，側(cè)面PAD⊥底面ABCD，E為PC的中點(diǎn)．
  （1）求證：BE⊥平面PCD；
  （2）若PA=PD，求二面角P-BC-D的余弦值．
  組卷：483引用：5難度：0.4

  解析