2022年八省八校（T8聯考）高考數學第二次聯考試卷（3月份）

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．復數z=i+

  1

  i

  ，則

  z

  =（　　）

  A．0

  B．2i

  C．-2i

  D．-1+i
  組卷：65引用：1難度：0.9

  解析

• 2．設集合A={x|log₂（x-1）＜2}，B={x|x＜5}，則（　　）

  A．A=B

  B．B?A

  C．A?B

  D．A∩B=?
  組卷：140引用：7難度：0.9

  解析

• 3．設S_n為等差數列{a_n}的前n項和，且滿足a₁＜0，S₃=S₉．則當S_n取得最小值時，n的值為（　　）

  A．3

  B．6

  C．9

  D．12
  組卷：206引用：2難度：0.7

  解析

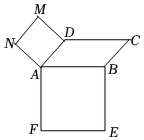• 4．如圖，在同一平面內沿平行四邊形ABCD兩邊AB，AD向外分別作正方形ABEF，ADMN，其中AB=2，AD=1，

  ∠

  BAD

  =

  π

  4

  ，則

  AC

  ?

  FN

  =（　　）

  A． - 2 2

  B． 2 2

  C．0

  D．-1
  組卷：248引用：4難度：0.8

  解析

• 5．若將函數

  f

  （

  x

  ）

  =

  2

  sin

  （

  2

  x

  -

  π

  3

  ）

  的圖象分別向左平移

  π

  3

  個單位長度與向右平移φ（φ＞0）個單位長度，所得的兩個函數圖象恰好重合，則φ的最小值為（　　）

  A． 2 3 π

  B． π 2

  C． 5 π 3

  D．π
  組卷：136引用：1難度：0.6

  解析

• 6．如圖，已知正四面體ABCD的棱長為1，過點B作截面α分別交側棱AC，AD于E，F兩點，且四面體ABEF的體積為四面體ABCD體積的

  1

  3

  ，則EF的最小值為（　　）

  A． 2 2

  B． 3 2

  C． 1 3

  D． 3 3
  組卷：387引用：5難度：0.6

  解析

• 7．黎曼函數是一個特殊的函數，由德國數學家波恩哈德?黎曼發現并提出，在高等數學中有著廣泛的應用．黎曼函數定義在[0，1]上，其解析式為：

  R

  （

  x

  ）

  =

  1 p ， 當 x = q p （ p , q 都是正整數 ， q p 是既約真分數 ）

  0 ， 當 x = 0 ， 1 或 [ 0 ， 1 ] 上的無理數

  ．若函數f（x）是定義在實數集上的偶函數，且對任意x都有f（2+x）+f（x）=0，當x∈[0，1]時，f（x）=R（x），則

  f

  （

  -

  ln

  2

  ）

  -

  f

  （

  2022

  5

  ）

  =（　　）

  A． 1 5

  B． 2 5

  C． - 2 5

  D． - 1 5
  組卷：107引用：1難度：0.7

  解析

四、解答題：本題共6小題，共70分．解答應寫出文字說明、證明過程或演算步驟．

• 21．已知雙曲線Γ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a＞0，b＞0）過點P（

  3

  ，

  6

  ），且Γ的漸近線方程為

  y

  =±

  3

  x

  ．
  （1）求Γ的方程；
  （2）如圖，過原點O作互相垂直的直線l₁，l₂分別交雙曲線于A，B兩點和C，D兩點，A，D在x軸同側．請從①②兩個問題中任選一個作答，如果多選，則按所選的第一個計分．
  ①求四邊形ACBD面積的取值范圍；
  ②設直線AD與兩漸近線分別交于M，N兩點，是否存在直線AD使M，N為線段AD的三等分點，若存在，求出直線AD的方程；若不存在，請說明理由．
  組卷：390引用：2難度：0.2

  解析

• 22．已知函數f（x）=（x²-ax）lnx+x（a∈R，a＞0）．
  （1）若1是函數f（x）的極值點，求a的值；
  （2）若0＜a≤1，試問f（x）是否存在零點．若存在，請求出該零點；若不存在，請說明理由．
  （3）若f（x）有兩個零點，求滿足題意的a的最小整數值．（參考數據：ln2≈0.693，

  e

  ≈

  1

  .

  649

  ）
  組卷：358引用：5難度：0.3

  解析