當前位置：試卷中心 > 試卷詳情

2021-2022學年江蘇省徐州市高二（下）期末數學試卷

發布：2025/1/7 22:0:3

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．已知向量
a
=
（
1
，
0
，
m
）
，
b
=
（
2
，
0
，-
2
3
）
，若
a
∥
b
，則
|
a
|
=（　　）
A．1 B．
2
C．
3
D．2
組卷：482引用：5難度：0.7
解析
2．對于數據2，6，8，3，3，4，6，8，四位同學得出了下列結論，正確的個數為（　　）
甲：平均數為5；
乙：沒有眾數；
丙：中位數是3；
丁：75百分位數是7．
A．1 B．2 C．3 D．4
組卷：37引用：1難度：0.8
解析
3．從1，2，3，4，5，6，7，8，9中不放回地依次取2個數，事件A為“第一次取到的數是偶數”，事件B為“第二次取到的數是奇數”，則P（B|A）=（　　）
A．
5
24
B．
5
16
C．
5
12
D．
5
8
組卷：110引用：4難度：0.8
解析
4．若
（
x
2
+
x
-
1
）
5
=
a
0
+
a
1
x
+
a
2
x
2
+
?
+
a
10
x
10
，則a₀+a₂+a₄+a₆+a₈+a₁₀=（　　）
A．-1 B．0 C．1 D．2
組卷：116引用：2難度：0.8
解析
5．3²⁰²²除以10的余數是（　　）
A．9 B．3 C．1 D．0
組卷：168引用：1難度：0.8
解析
6．已知直線l過點A（1，-1，-1），且方向向量為
m
=
（
1
，
0
，-
1
）
，則點P（1，1，1）到l的距離為（　　）
A．
2
2
B．
6
C．
3
D．
2
組卷：1708引用：6難度：0.7
解析
7．某班將6名同學分配到甲、乙、丙三個社區參加勞動鍛煉，每個社區至少分配一名同學，則甲社區恰好分配2名同學的方法共有（　　）
A．105種 B．150種 C．210種 D．660種
組卷：109引用：2難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題6小題，共70分，解答應寫出文字明、證明過程或演算步驟．

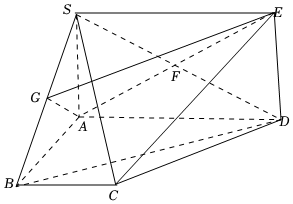21．如圖，已知SA垂直于梯形ABCD所在的平面，矩形SADE的對角線交于點F，G為SB的中點，
∠
ABC
=∠
BAD
=
π
2
，
SA
=
AB
=
BC
=
1
2
AD
=
1
．
（1）求證：BD∥平面AEG；
（2）求二面角C-SD-E的余弦值；
（3）在線段EG上是否存在一點H，使得BH與平面SCD所成角的大小為
π
6
？若存在，求出GH的長；若不存在，說明理由．
組卷：266引用：8難度：0.4
解析
22．為搶占市場，某品牌電動汽車近期進行了一系列優惠促銷方案．要保證品質兼優，在車輛出廠前抽取100輛M款汽車作為樣本進行了單次最大續航里程的測試．現對測試數據進行分析，得到如圖所示的頻率直方圖：

（1）估計這100輛汽車的單次最大續航里程的平均值
x
（同一組中的數據用該組區間的中點值作代表）；
（2）根據大量的測試數據，可以認為這款汽車的單次最大續航里程X近似地服從正態分布N（μ，σ²），經計算樣本標準差s的近似值為50．用樣本平均數
x
作為μ的近似值，用樣本標準差s作為σ的估計值，現從生產線下任取一輛汽車，求它的單次最大續航里程恰在220千米到470千米之間的概率；
（3）為迅速搶占市場舉行促銷活動，銷售公司現面向意向客戶推出“玩游戲，贏大獎，送汽車模型”活動，客戶可根據拋擲骰子向上的點數，遙控汽車模型在方格圖上行進，若汽車模型最終停在“幸運之神”方格，則可獲得購車優惠券2萬元；若最終停在“贈送汽車模型”方格，則可獲得汽車模型一個．方格圖上標有第0格、第1格、第2格、…、第20格．汽車模型開始在第0格，客戶每擲一次骰子，汽車模型向前移動一次．若擲出1，2，3，4點，汽車模型向前移動一格（從第k格到第k+1格），若擲出5，6點，汽車模型向前移動兩格（從第k格到第k+2格），直到移到第19格（幸運之神）或第20格（贈送汽車模型）時游戲結束．設汽車模型移到第n（1≤n≤19）格的概率為P_n．
（ⅰ）求P₁₉；
（ⅱ）若有6人玩該游戲，每人一局，求這6人獲得優惠券總金額的期望（結果精確到1萬元）．
附：若隨機變量X服從正態分布N（μ，σ²），則P（|X-μ|＜σ）≈0.6827，P（|X-μ|＜2σ）≈0.9545，P（|X-μ|＜3σ））≈0.9973．
組卷：299引用：1難度：0.5
解析