2022-2023學(xué)年寧夏中衛(wèi)中學(xué)高二（下）第二次月考數(shù)學(xué)試卷（理科）（A卷）

一、選擇題（本大題共12個小題，每小題5分，共60分．每小題給出的選項中，只有一項是符合題目要求的，請將正確的答案涂到答題卡上）

• 1．設(shè)復(fù)數(shù)z滿足

  z

  1

  -

  i

  =1+2i,則

  z

  的虛部為（　　）

  A．-1

  B．1

  C．-i

  D．i
  組卷：221引用：6難度：0.8

  解析

• 2．拋物線y=x²在點M（

  1

  2

  ，

  1

  4

  ）的切線的傾斜角是（　　）

  A．30°

  B．45°

  C．60°

  D．90°
  組卷：28引用：4難度：0.9

  解析

• 3．已知向量

  a

  =

  （

  2

  ，

  1

  ，

  2

  ）

  ，

  b

  =

  （

  -

  2

  ，

  x

  ,

  2

  ）

  ，

  c

  =

  （

  4

  ，-

  2

  ，

  3

  ）

  ，若

  b

  ⊥

  （

  a

  +

  c

  ）

  ，則x的值為（　　）

  A．-2

  B．2

  C．-6

  D．6
  組卷：97引用：3難度：0.8

  解析

• 4．《聊齋志異》中有這樣一首詩：“挑水砍柴不堪苦，請歸但求穿墻術(shù)．得訣自詡無所阻，額上墳起終不悟．”在這里，我們稱形如以下形式的等式具有“穿墻術(shù)”：
  2

  2

  3

  =

  2

  2

  3

  ，3

  3

  8

  =

  3

  3

  8

  ，4

  4

  15

  =

  4

  4

  15

  ，5

  5

  24

  =

  5

  5

  24

  
  則按照以上規(guī)律，若8

  8

  n

  =

  8

  8

  n

  具有“穿墻術(shù)”，則n=（　　）

  A．7

  B．35

  C．48

  D．63
  組卷：428引用：41難度：0.9

  解析

• 5．已知函數(shù)f（x）=e^x-ax,則“a＜-3”是“函數(shù)f（x）在R上為增函數(shù)”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：41引用：4難度：0.6

  解析

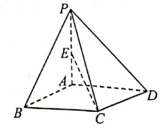• 6．在《九章算術(shù)》中，將底面為矩形且有一條側(cè)棱與底面垂直的四棱錐稱為“陽馬”．如圖，四棱錐P-ABCD為陽馬，側(cè)棱PA⊥底面ABCD，PA=AB=AD，E為棱PA的中點，則直線CE與平面PAD所成角的正弦值為（　　）

  A． 2 3

  B． 5 3

  C． 3 2

  D． 2 2
  組卷：1168引用：12難度：0.5

  解析

• 7．

  ∫

  2

  -

  2

  （

  4

  -

  x

  2

  +

  x

  2

  ）

  dx

  =（　　）

  A．2π

  B．8

  C． π 2 + 16 3

  D． 2 π + 16 3
  組卷：49引用：3難度：0.8

  解析

三、解答題：（本大題共6小題，滿分70分。解答須寫出文字說明，證明過程或演算步驟）

• 21．已知拋物線C：y²=2px（p＞0）的焦點為F，傾斜角為45°的直線l過點F與拋物線C交于A，B兩點，且|AB|=8．
  （1）求p；
  （2）設(shè)點E為直線x=

  p

  2

  與拋物線C在第一象限的交點，過點E作C的斜率分別為k₁，k₂的兩條弦EM，EN，如果k₁+k₂=-1，證明直線MN過定點，并求出定點坐標．
  組卷：231引用：3難度：0.7

  解析

• 22．設(shè)函數(shù)f（x）=e^x-ax-2．
  （1）求f（x）的單調(diào)區(qū)間；
  （2）若a=1，k為整數(shù)，且當x＞0時，（x-k）f′（x）+x+1≥0，求k的最大值．
  組卷：158引用：1難度：0.4

  解析