當前位置：試卷中心 > 試卷詳情

2023-2024學年江蘇省宿遷市沭陽縣九年級（上）月考數學試卷（9月份）

發布：2024/9/4 6:0:10

一、選擇題。（本大題共有8小題，每小題3分，共24分。在每小題給出的四個選項中，只有一項是符合題目要求的。）

1．下列方程中，關于x的一元二次方程的是（　　）
A．x+y=1 B．3x+y²=2 C．2x-x²=3 D．x+
1
x
=4
組卷：64引用：8難度：0.8
解析
2．用配方法解方程x²-4x-4=0時，原方程應變形為（　　）
A．（x-2）²=0 B．（x-2）²=8 C．（x+2）²=0 D．（x+2）²=8
組卷：927引用：21難度：0.8
解析
3．⊙O的半徑為3，點A到圓心O的距離為4，點A與⊙O的位置關系是（　　）
A．點A在⊙O外 B．點A在⊙O內 C．點A在⊙O上 D．不能確定
組卷：210引用：10難度：0.9
解析
4．若關于x的一元二次方程x²+3x+4=0，該方程的解的情況是（　　）
A．沒有實數根 B．有兩個不相等的實數根
C．有兩個相等的實數根 D．不能確定
組卷：317引用：8難度：0.6
解析
5．下列結論正確的是（　　）
A．三點確定一個圓
B．相等的圓心角所對的弧相等
C．等弧所對的弦相等
D．三角形的外心到三角形各邊的距離相等
組卷：235引用：3難度：0.6
解析
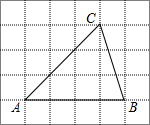6．如圖，將△ABC放在每個小正方形邊長為1的網格中，點A、B、C均落在格點上，用一個圓面去覆蓋△ABC，能夠完全覆蓋這個三角形的最小圓面半徑是（　　）
A．
5
B．
6
C．2 D．
5
2
組卷：2839引用：26難度：0.9
解析
7．已知3是關于x的方程x²-（m+1）x+2m=0的一個實數根，并且這個方程的兩個實數根恰好是等腰△ABC的兩條邊的邊長，則△ABC的周長為（　　）
A．7 B．10 C．11 D．10或11
組卷：9548引用：54難度：0.7
解析
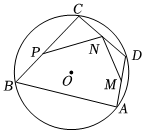8．如圖，AB，BC是⊙O的弦，∠B=60°，點O在∠B內，點D為
?
AC
上的動點，點M，N，P分別是AD，DC，CB的中點．若⊙O的半徑為6，則PN+MN的長度的最大值是（　　）
A．6 B．12 C．
3
+
3
3
D．
6
+
3
3
組卷：498引用：1難度：0.5
解析

二、填空題。（本大題共10小題，每小題3分，共30分，不需要寫出解答過程。）

9．一元二次方程x²=x的根
．
組卷：436引用：95難度：0.9
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題。（本題共10小題，共96分。解答時寫出必要的文字說明、證明過程或演算步驟）

27．探索一個問題：任意給定一個矩形A，是否存在另一個矩形B，它的周長和面積分別是已知矩形周長和面積的一半（完成下列空格）．
（1）當已知矩形A的邊長分別是6和1時，小亮同學是這樣研究的：設所求矩形的兩邊分別是x,y,由題意得方程組
x
+
y
=
7
2
xy
=
3
，消去y化簡得2x²-7x+6=0：
∵Δ=49-48＞0，x₁=
；x₂=
；所以滿足要求的B存在；
（2）如果已知矩形A的邊長分別是2和1，請你仿照小亮方法研究是否存在滿足要求的矩形B；
（3）如果矩形A的邊長為m,n,請你研究滿足什么條件時，矩形B存在？
組卷：295引用：7難度：0.6
解析
28．（1）【基礎鞏固】如圖1，△ABC內接于⊙O，若∠C=60°，弦AB=4
3
，則半徑r=
；
（2）【問題探究】如圖2，四邊形ABCD的四個頂點均在⊙O上，若∠ADC=60°，AD=DC，點B為弧AC上一動點（不與點A，點C重合）．求證：AB+BC=BD；
（3）【解決問題】如圖3，一塊空地由三條直路（線段AD、AB、BC）和一條道路劣弧
?
CD
圍成，已知CM=DM=
3
千米，∠DMC=60°，
?
CD
的半徑為1千米，市政府準備將這塊空地規劃為一個公園，主入口在點M處，另外三個入口分別在點C、D、P處，其中點P在
?
CD
上，并在公園中修四條慢跑道，即圖中的線段DM、MC、CP、PD，某數學興趣小組探究后發現C、P、D、M四個點在同一個圓上，請你幫他們證明C、P、D、M四點共圓，并判斷是否存在一種規劃方案，使得四條慢跑道總長度（即四邊形DMCP的周長）最大？若存在，求其最大值；若不存在，說明理由．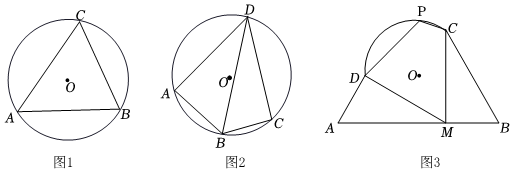
?
組卷：309引用：5難度：0.1
解析