人教A版（2019）必修第一冊《2.3 二次函數與一元二次方程、不等式》2021年同步練習卷（11）

一、單選題

• 1．不等式x²-4x+3＜0的解集是（　　）

  A．{x|1＜x＜3}

  B．{x|x＜0}

  C．{x|x＜5}

  D．{x|x＞7}
  組卷：118引用：3難度：0.7

  解析

• 2．已知不等式x²+ax+4＞0的解集為R，則a的取值范圍是（　　）

  A．[-4，4]	B．（-4，4）
  C．（-∞，-4]∪[4，+∞）	D．（-∞，-4）∪[4，+∞）
  組卷：38引用：1難度：0.7

  解析

• 3．不等式ax²-x+c＞0的解集為{x|-2＜x＜1}，則函數y=ax²+x+c的圖象大致為（　　）

  A．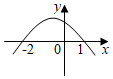

  B．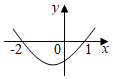

  C．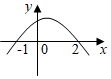

  D．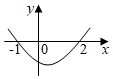
  組卷：235引用：29難度：0.9

  解析

• 4．設集合M={x||x|≤2}，N={x|x²-2x-3＜0}，則集合M∩N=（　　）

  A．{x|-1≤x＜2}

  B．{x|-1＜x≤2}

  C．{x|-2＜x≤3}

  D．{x|-2≤x＜3}
  組卷：123引用：3難度：0.8

  解析

• 5．已知命題p：?x∈R，x²+a＜0，那么“a≤0”是“p為真命題”的（　　）條件．

  A．充分不必要	B．必要不充分
  C．充要	D．既不充分也不必要
  組卷：330引用：2難度：0.7

  解析

• 6．若“?x∈R，使得x²-mx+1＜0”是假命題，則實數m的取值范圍是（　　）

  A．（-2，2）	B．[-2，2]
  C．（-∞，-2）∪（2，+∞）	D．（-∞，-2]∪[2，+∞）
  組卷：52引用：2難度：0.7

  解析

• 7．已知集合A={x|x²+4x-12≤0}，B={x|x＜a}，若集合A?B，則實數a的取值范圍是（　　）

  A．（-6，+∞）

  B．[-6，+∞）

  C．（2，+∞）

  D．[2，+∞）
  組卷：772引用：3難度：0.7

  解析

四、解答題

• 21．已知命題：“?x∈R，x²-x-m＞0恒成立“是真命題，
  （1）求實數m的取值集合B；
  （2）設不等式（x-3a）（x-a-2）＜0的解集為A，若A∪B=B，求實數a的取值范圍．
  組卷：55引用：2難度：0.5

  解析

• 22．已知函數f（x）=x²+2x+1．
  （1）求關于x的不等式f（x）≥b²（b≥0）的解集；
  （2）若不等式[f（x）]²-2mf（x）+m²-1≥0對于任意x∈[-3，2]都成立，求m的取值范圍．
  組卷：90引用：2難度：0.5

  解析