2022-2023學年北京市東城區高二（上）期末數學試卷

一、選擇題共12小題，每小題3分，共36分。在每個小題列出的四個選項中，選出符合題目要求的一項。

• 1．已知向量

  a

  =（8，-2，1），

  b

  =（-4，1，k），且

  a

  ∥

  b

  ，那么實數k的值為（　　）

  A． 1 2

  B． - 1 2

  C．-2

  D．2
  組卷：600引用：7難度：0.7

  解析

• 2．直線

  l

  ：

  x

  -

  y

  -

  3

  =

  0

  的傾斜角是（　　）

  A．45°

  B．135°

  C．60°

  D．90°
  組卷：164引用：1難度：0.9

  解析

• 3．拋物線y²=-2x的準線方程是（　　）

  A． y = 1 2

  B．y=-1

  C． x = 1 2

  D．x=1
  組卷：188引用：3難度：0.7

  解析

• 4．2021年9月17日，北京2022年冬奧會和冬殘奧會主題口號正式對外發布——“一起向未來”（英文為：“TogetherforaSharedFuture”），這是中國向世界發出的誠摯邀約，傳遞出14億中國人民的美好期待．“一起向未來”的英文表達是：“TogetherforaSharedFuture”，其字母出現頻數統計如表：
  

  字母	t	o	g	e	h	r	f	a	s	d	u
  頻數	3	2	1	4	2	4	2	2	1	1	2

  合計頻數為24，那么字母“e”出現的頻率是（　　）

  A． 1 8

  B． 1 6

  C． 1 12

  D． 1 4
  組卷：91引用：1難度：0.8

  解析

• 5．設S_n為數列{a_n}的前n項和，已知a₁=3，S_n+1=S_n+2ⁿ，那么a₃=（　　）

  A．4

  B．5

  C．7

  D．9
  組卷：439引用：1難度：0.7

  解析

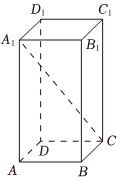• 6．已知在長方體ABCD-A₁B₁C₁D₁中，AB=AD=1，AA₁=2，那么直線A₁C與平面AA₁D₁D所成角的正弦值為（　　）

  A． 6 6

  B． 35 6

  C． 3 3

  D． 6 3
  組卷：620引用：4難度：0.6

  解析

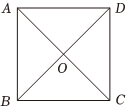• 7．如圖，點O是正方形ABCD兩條對角線的交點．從這個正方形的四個頂點中隨機選取兩個，那么這兩個點關于點O對稱的概率為（　　）

  A． 1 5

  B． 1 4

  C． 1 3

  D． 1 2
  組卷：129引用：1難度：0.8

  解析

三、解答題共5小題，共46分。解答應寫出文字說明、證明過程或演算步驟。

• 22．已知橢圓E：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的離心率為

  2

  2

  ，一個頂點為A（0，1）．
  （Ⅰ）求橢圓E的方程；
  （Ⅱ）若求點A的直線l與橢圓E的另一個交點為B，且|AB|=

  4

  3

  2

  ，求點B的坐標．
  組卷：453引用：2難度：0.6

  解析

• 23．已知無窮數列{y_n}滿足公式y_n+1=

  2 y n ， 0 ≤ y n ＜ 1 2 ，

  2 - 2 y n ， 1 2 ≤ y n ≤ 1 ．

  設y₁=a（0≤a≤1）．
  （Ⅰ）若a=

  1

  4

  ，求y₃的值；
  （Ⅱ）若y₃=0，求a的值；
  （Ⅲ）給定整數M（M≥3），是否存在這樣的實數a,使數列{y_n}滿足：
  ①數列{y_n}的前M項都不為零；
  ②數列{y_n}中從第M+1項起，每一項都是零．
  若存在，請將所有這樣的實數a從小到大排列形成數列{a_n}，并寫出數列{a_n}的通項公式；若不存在，請說明理由．
  組卷：117引用：2難度：0.3

  解析