2023-2024學年福建省福州四十中八年級（上）第一次適應性數學試卷

一.選擇題（每題4分，共40分）

• 1．下列各組數可能是一個三角形的邊長的是（　　）

  A．4，4，9

  B．3，4，5

  C．2，6，8

  D．1，2，3
  組卷：284引用：29難度：0.6

  解析

• 2．若△ABC的三個內角之比為2：3：5，則△ABC一定是（　　）

  A．銳角三角形

  B．直角三角形

  C．鈍角三角形

  D．等腰三角形
  組卷：244引用：3難度：0.7

  解析

• 3．若一個多邊形的內角和為1080°，則這個多邊形的邊數為（　　）

  A．6

  B．7

  C．8

  D．9
  組卷：3030引用：262難度：0.9

  解析

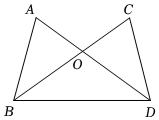• 4．如圖，AD，BC相交于點O，∠A=∠C，要根據“ASA”證明△AOB≌△COD，還需添加的一個條件是（　　）

  A．AB=CD

  B．AO=CO

  C．BO=DO

  D．∠ABO=∠CDO
  組卷：216引用：4難度：0.7

  解析

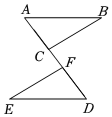• 5．如圖，△ABC≌△DEF，圖中和AF相等的線段（　　）

  A．線段BC

  B．線段AB

  C．線段CD

  D．線段DE
  組卷：83引用：4難度：0.7

  解析

• 6．如圖所示，是一塊三角形的草坪，現要在草坪上建一涼亭供大家休息，要使涼亭到草坪三條邊的距離相等，涼亭的位置應選在（　　）

  A．△ABC的三條中線的交點

  B．△ABC三條角平分線的交點

  C．△ABC三條高所在直線的交點

  D．△ABC三邊的中垂線的交點
  組卷：7358引用：61難度：0.9

  解析

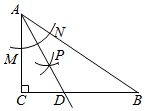• 7．如圖，在△ABC中，∠C=90°，以A為圓心，任意長為半徑畫弧，分別交AC、AB于點M，N，再以M、N為圓心，大于

  1

  2

  MN的長為半徑作弧，兩弧交于點P，作射線AP交BC于點D，若AB=3

  3

  ，CD=2，則S_△ADB=（　　）

  A．2

  B．2 3

  C．3 3

  D．4 3
  組卷：400引用：3難度：0.7

  解析

• 8．如圖，在△MPN中，H是高MQ和NR的交點，且MQ=NQ，已知PQ=5，NQ=9，則MH長為（　　）

  A．3

  B．4

  C．5

  D．6
  組卷：2392引用：18難度：0.7

  解析

三.解答題（共9小題，共86分）

• 25．在△ABC中，AB=AC，點D是直線BC上一點（不與B、C重合），以AD為一邊在AD的右側作△ADE，使AD=AE，∠DAE=∠BAC，連接CE． 
  （1）如圖1，當點D在線段BC上，如果∠BAC=90°，求∠BCE的度數；
  （2）設∠BAC=α，∠BCE=β．如圖2，當點D在線段BC上移動，則α，β之間有怎樣的數量關系？請直接寫出你的結論．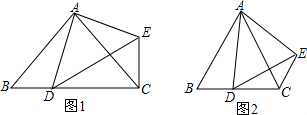
  
  組卷：358引用：6難度：0.3

  解析

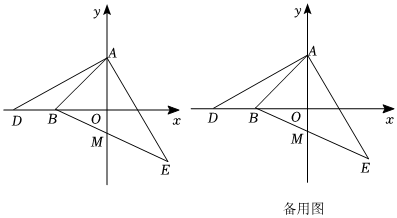• 26．如圖，A點的坐標為（0，a），B點的坐標為（b,0），且

  |

  a

  -

  4

  |

  +

  b

  +

  4

  =

  0

  ，D為x軸上的一個動點，AE⊥AD，且AE=AD，連接BE交y軸于點M．
  （1）求A，B兩點坐標．
  （2）若D點的坐標為（-5，0），求E點的坐標．
  （3）當D點在x軸上運動時，求證：

  OM

  BD

  為定值．
  組卷：111引用：1難度：0.3

  解析