2022-2023學年重慶市南川區九年級（上）期末數學試卷

一、選擇題（本大題12個小題，每小題4分，共48分）在每個小題的下面，都給出了代號為A、B、C、D的四個答案，其中只有一個是正確的，請將答題卡上題號右側正確答案所對應的方框涂黑．

• 1．點（3，-2）關于原點對稱的點的坐標為（　　）

  A．（-3，2）

  B．（-3，-2）

  C．（3，2）

  D．（-2，3）
  組卷：226引用：6難度：0.8

  解析

• 2．下列事件為必然事件的是（　　）

  A．太陽從東方升起

  B．射擊運動員射擊一次，命中靶心

  C．購買一張彩票中獎一百萬元

  D．籃球隊員在罰球線上投籃一次，未投中
  組卷：43引用：2難度：0.9

  解析

• 3．拋物線y=3（x+2）²-1的頂點坐標是（　　）

  A．（2，-1）

  B．（2，1）

  C．（-2，1）

  D．（-2，-1）
  組卷：170引用：3難度：0.7

  解析

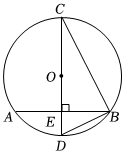• 4．如圖，CD是⊙O的直徑，弦AB⊥CD于E，連接BC、BD，下列結論中不一定正確的是（　　）

  A．AE=BE

  B． ? AD = ? BD

  C．OE=DE

  D．∠DBC=90°
  組卷：1125引用：83難度：0.7

  解析

• 5．一個布袋里裝有8個只有顏色不同的球，其中2個紅球，6個白球．從布袋里任意摸出1個球，則摸出的球是白球的概率為（　　）

  A． 3 4

  B． 1 4

  C． 1 3

  D． 1 5
  組卷：46引用：2難度：0.7

  解析

• 6．一元二次方程x²-2x+3=0的根的情況是（　　）

  A．有兩個不相等的實數根	B．有兩個相等的實數根
  C．只有一個實數根	D．沒有實數根
  組卷：200引用：5難度：0.6

  解析

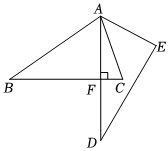• 7．如圖，將△ABC繞點A逆時針旋轉50°得到△ADE，若∠E=70°且AD⊥BC于點F，則∠BAC的度數為（　　）

  A．65°

  B．70°

  C．75°

  D．80°
  組卷：590引用：10難度：0.7

  解析

• 8．已知點A（-2，y₁），B（1，y₂），C（3，y₃），都在函數

  y

  =

  3

  x

  的圖象上，則y₁、y₂、y₃的大小關系是（　　）

  A．y1＞y3＞y2

  B．y1＞y2＞y3

  C．y2＞y1＞y3

  D．y2＞y3＞y1
  組卷：224引用：4難度：0.7

  解析

四、解答題（本題7個小題，每小題10分，共70分）解答時必須給出必要的演算過程或推理步驟，畫出必要的圖形（包括輔助線），請將解答過程書寫在答題卡中對應的位置上．

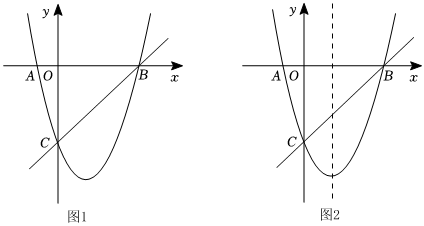
• 24．如圖1，在平面直角坐標系中，二次函數y=ax²+bx-3（a≠0）的圖象與x軸于A（-1，0），B（3，0）兩點，與y軸交于C點，點P是直線BC下方拋物線上一動點．
  
  （1）求這個二次函數的解析式；
  （2）當動點P運動到什么位置時，使四邊形ACPB的面積最大，求出此時四邊形ACPB的面積最大值和P的坐標；
  （3）如圖2，點M在拋物線對稱軸上，點N是平面內一點，是否存在這樣的點M、N，使得以點M、N、A、C為頂點的四邊形是菱形？若存在，請直接寫出所有M點的坐標；若不存在，請說明理由．
  組卷：1195引用：4難度：0.6

  解析

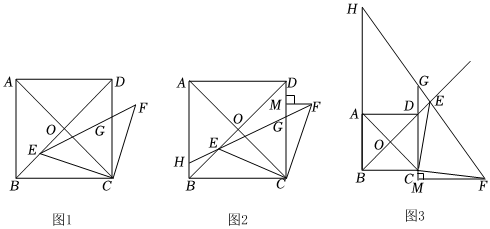
• 25．如圖1，在正方形ABCD中，對角線AC、BD相交于點O，點E為線段BO上一點，連接CE，將CE繞點C順時針旋轉90°得到CF，連接EF交CD于點G．
  
  （1）若AB=8，BE=2

  2

  ，求△CEF的面積．
  （2）如圖2，線段FE的延長線交AB于點H，過點F作FM⊥CD于點M，求證：BH+MG=

  2

  2

  BE；
  （3）如圖3，點E為射線OD上一點，線段FE的延長線交直線CD于點G，交直線AB于點H，過點F作FM垂直直線CD于點M，請直接寫出線段BH、MG、BE的數量關系．
  組卷：339引用：2難度：0.1

  解析