2008-2009學年湖南省長沙市長郡中學高三（上）12月周考數學試卷（文科）（4）

一．選擇題：本大題共10小題，每小題5分，共50分．

• 1．若集合A={x|x²-5x+4≤0}，B={x||x-a|＜1}，則“a∈（2，3）”是“B?A”的（　　）

  A．充分但不必要條件	B．必要但不充分條件
  C．充要條件	D．既不充分又不必要條件
  組卷：68引用：16難度：0.9

  解析

• 2．200輛汽車經過某一雷達地區，時速頻率分布直方圖如圖所示，則時速超過60km/h的汽車數量為（　　）
  

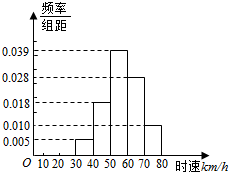
  A．65輛

  B．76輛

  C．88輛

  D．95輛
  組卷：57引用：22難度：0.9

  解析

• 3．已知數列{a_n}為等差數列，S_n為{a_n}的前n項和，a₇=4，則S₁₁-S₂的值為（　　）

  A．9

  B．18

  C．36

  D．72
  組卷：14引用：2難度：0.9

  解析

• 4．設f （x）=

  0 （ x 為有理數 ）

  1 （ x 為無理數 ）

  ，則f（f（x））（x∈R） 的值為（　　）

  A．0

  B．1

  C．0或1

  D．以上都不對
  組卷：111引用：1難度：0.9

  解析

• 5．已知圓的半徑為4，a、b、c為該圓的內接三角形的三邊，若abc=16

  2

  ，則三角形的面積為（　　）

  A．2 2

  B．8 2

  C． 2

  D． 2 2
  組卷：448引用：20難度：0.9

  解析

• 6．設a∈R，函數f（x）=x³+ax²+（a-3）x的導函數是f′（x），若f′（x）是偶函數，則曲線y=f（x）在原點處的切線方程為（　　）

  A．y=-3x

  B．y=-2x

  C．y=3x

  D．y=2x
  組卷：238引用：19難度：0.7

  解析

• 7．我們把使得f（x）=0的實數x叫做函數y=f（x）的零點，對于區間[a,b]上的連續函數y=f（x），若f（a）?f（b）＜0，那么函數y=f（x）在區間（a,b）內有零點，則函數f（x）=lgx-

  2

  x

  的零點所在的區間應是（　　）

  A．（1，2）

  B．（2，3）

  C．（3，4）

  D．（4，5）
  組卷：44引用：1難度：0.7

  解析

三．解答題：本大題共6小題，共75分，解答應寫出文字說明、證明過程或演算步驟．

• 20．已知定義在[0，1]的函數f（x）同時滿足以下三條：①對任意的x∈[0，1]，總有f（x）≥0；②f（1）=1；③當x₁≥0，x₂≥0，x₁+x₂≤1時，總有f（x₁+x₂）≥f（x₁）+f（x₂）成立．
  （1）函數g（x）=2^x-1在區間[0，1]上是否同時適合①②③？并說明理由；
  （2）設m,n∈[0，1]，且m＞n,試比較f（m）與f（n）的大小；
  （3）假設存在a∈[0，1]，使得f（a）∈[0，1]且f[f（a）]=a,求證：f（a）=a.
  組卷：19引用：1難度：0.3

  解析

• 21．已知等差數列{x_n}，S_n是{x_n}的前n項和，且x₃=5，S₅+x₅=34
  （1）求{x_n}的通項公式；
  （2）判別方程sin²x_n+x_ncosx_n+1=S_n是否有解，說明理由．
  （3）設a_n=（

  1

  3

  ）ⁿ，T_n是{a_n}前n項和，是否存在正數λ，對任意正整數n,k,使T_n-λ

  x

  2

  k

  ＜λ²恒成立？若存在，求λ的取值范圍；若不存在，說明理由．
  組卷：16引用：1難度：0.1

  解析