2021-2022學年廣東省佛山一中高一（下）期中數學試卷

一、單選題（本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.）

• 1．復數z=

  i

  1

  -

  i

  （i為虛數單位）在復平面內對應的點位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：108引用：12難度：0.9

  解析

• 2．已知向量

  m

  =（2a,-1），

  n

  =（3，a+2），若

  m

  ⊥

  n

  ，則a=（　　）

  A．1

  B． 3 5

  C． 1 3

  D． 2 5
  組卷：227引用：5難度：0.8

  解析

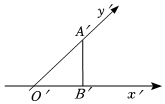• 3．如圖所示，一個水平放置的三角形的斜二測直觀圖是等腰直角三角形A'B'O'，若O'B'=1，那么原三角形ABO的面積是（　　）

  A． 1 2

  B． 2 2

  C． 2

  D．2 2
  組卷：52引用：2難度：0.7

  解析

• 4．已知角θ的終邊過點（1，-1），

  cos

  （

  π

  2

  +

  θ

  ）

  =（　　）

  A． - 2 2

  B． 2 2

  C． - 1 2

  D． 1 2
  組卷：235引用：2難度：0.8

  解析

• 5．在△ABC中，角A，B，C的對邊分別為a,b,c,且

  co

  s

  2

  A

  2

  =

  c

  +

  b

  2

  c

  ，則△ABC的形狀為（　　）

  A．等邊三角形	B．直角三角形
  C．等腰三角形	D．等腰直角三角形
  組卷：125引用：5難度：0.8

  解析

• 6．函數

  f

  （

  x

  ）

  =

  sin

  （

  ωx

  +

  φ

  ）

  （

  A

  ＞

  0

  ，

  ω

  ＞

  0

  ，

  |

  φ

  |

  ＜

  π

  2

  ）

  的部分圖象如圖所示，則（　　）

  A． f （ x ） = sin （ 4 x + π 3 ）	B． f （ x ） = sin （ 4 x - π 6 ）
  C． f （ x ） = sin （ 2 x + π 3 ）	D． f （ x ） = sin （ 2 x - π 3 ）
  組卷：234引用：5難度：0.7

  解析

• 7．在△ABC中，設

  AC

  ²-

  AB

  ²=2

  AM

  ?

  BC

  ，那么動點M形成的圖形必通過△ABC的（　　）

  A．垂心

  B．內心

  C．外心

  D．重心
  組卷：483引用：5難度：0.6

  解析

四、解答題（本大題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.）

• 21．如圖，在△ABC中，AB⊥AC，AB=AC=2，點E，F是線段BC（含端點）上的動點，且點E在點F的右下方，在運動的過程中，始終保持∠EAF=

  π

  4

  不變，設∠EAB=θ弧度．
  （1）寫出θ的取值范圍，并分別求線段AE，AF關于θ的函數關系式；
  （2）求△EAF面積S的最小值．
  組卷：334引用：4難度：0.7

  解析

• 22．已知函數f（x）=a（|sinx|+|cosx|）+4sin2x+9，且

  f

  （

  π

  4

  ）

  =

  13

  -

  9

  2

  ．
  （1）求a的值；
  （2）求出f（x）的最小正周期，并證明；（“周期”要證，“最小”不用證明）
  （3）是否存在正整數n,使得f（x）在區(qū)間[0，nπ]內恰有2021個零點，若存在，求出n的值；若不存在，說明理由．
  組卷：69引用：2難度：0.4

  解析