2022-2023學年重慶八中宏帆中學九年級（上）第二次定時作業數學試卷
發布：2024/8/24 8:0:8
一、選擇題（本大題共10個小題）在每個小題的下面，都給出了代號為A、B、C、D的四個答案，請將正確答案的代號填涂在答題卡上的相應位置．
-
1．下列圖案中，是軸對稱圖形的是（ ）
組卷：5引用：1難度：0.9 -
2．下列計算正確的是（ ）
組卷：1218引用：17難度：0.8 -
3．甲、乙、丙、丁四人進行射擊測試，每人10次射擊成績的平均數都為9.0環，方差分別為s甲2=0.63，s乙2=0.51，s丙2=0.42，s丁2=0.48，則四人中成績最穩定的是（ ）
組卷：98引用：5難度：0.7 -
4．已知一個直角三角形的兩條邊長分別是6和8，則第三邊長是（ ）
組卷：515引用：8難度：0.9 -
5．若2、5、n為三角形的三邊長，則化簡
+（3-n）2的結果為（ ）（8-n）2組卷：1840引用：5難度：0.5 -
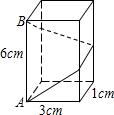6．如圖，長方體的底面邊長為1cm和3cm,高為6cm.如果用一根細線從點A開始經過4個側面纏繞一圈到達B，那么所用細線最短需要（ ）組卷：4388引用：25難度：0.9 -
7．為考查兩名實習工人的工作情況，質檢部將他們工作第一周每天生產合格產品的個數整理成甲，乙兩組數據，如下表：
關于以上數據，下列說法正確的有（ ）個．甲 2 6 7 7 8 乙 2 3 4 8 8
①甲、乙的眾數相同；
②甲、乙的中位數相同；
③甲的平均數小于乙的平均數．組卷：16引用：1難度：0.7 -
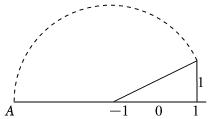8．如圖，在數軸上以-1表示的點為圓心，以直角三角形的斜邊為半徑作出一條圓弧（虛線），該圓弧與數軸交于點A，點A所表示的數為m,則m的值為（ ）組卷：126引用：3難度：0.6 -
9．勾股定理是一個古老的數學定理，它有很多種證明方法，如圖所示四幅幾何圖形中，不能用于證明勾股定理的是（ ）
組卷：1207引用：4難度：0.5
六、解答題（本大題共3個小題）解答時每小題必須給出必要的演算過程或推理步驟，畫出必要的圖形（包括輔助線），請將解答過程書寫在答題卡中對應的位置上．
-
27．一個四位正整數A的千位上的數字小于十位上的數字，且千位上的數字與百位上的數字之和等于十位上的數字與個位上的數字之和，均等于10，則稱A為“十全十美數”，將“十全十美數”A的千位和百位數字組成的兩位數與十位和個位數字組成的兩位數的和記為F（A），將“十全十美數”A的千位和十位數字組成的兩位數與百位和個位數字組成的兩位數的差記為G（A）．
例如：四位正整數2873，
∵2+8=7+3=10，且2＜7
∴2873是“十全十美數”，
此時，F（A）=28+73=101，G（A）=27-83=-56．
（1）若M是最大的“十全十美數”，請直接寫出：M=，F（M）=，G（M）=；
（2）若A是“十全十美數”，且2F（A）+G（A）能被9整除，求所有符合條件的A的值．組卷：390引用：2難度：0.5 -
28．在△ABC中，AB=AC，E是BC中點．
（1）如圖1，若△ABC是銳角三角形，AB=13，BC=10，AC邊上的高EM=；
（2）G、H分別為射線BA、AC上一點，且滿足∠GEH+∠BAC=180°．
①如圖2，若△ABC是直角三角形，∠A=90°，且G、H分別在線段BA、AC上，判斷線段HE和GE的關系，并說明理由；
②如圖3，若△ABC是鈍角三角形，∠BAC＞90°，連接AE并延長至點D，使DE=AE，過點E作EF⊥BD于點F，當點G、H分別在線段BA、AC延長線上時，求證：2BF+CH=BG．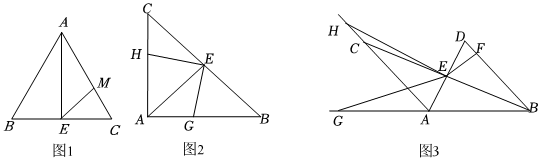
組卷：51引用：1難度：0.2