2023年江蘇省鎮江市丹陽市中考數學模擬試卷

一.填空題（共12小題，每小題2分，共24分）

• 1．-2023的絕對值是

  ．
  組卷：468引用：17難度：0.8

  解析

• 2．二次根式

  x

  -

  1

  有意義的條件是

  ．
  組卷：736引用：12難度：0.8

  解析

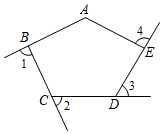• 3．如圖，五邊形ABCDE中，∠A=125°，則∠1+∠2+∠3+∠4的度數是

  ．
  組卷：1378引用：15難度：0.8

  解析

• 4．為了踐行“首都市民衛生健康公約”，某班級舉辦“七步洗手法”比賽活動，小明的單項成績如表所示（各項成績均按百分制計）：

  項目	書面測試	實際操作	宣傳展示
  成績（分）	96	98	96

  若按書面測試占30%、實際操作占50%、宣傳展示占20%，計算參賽個人的綜合成績（百分制），則小明的最后得分是

  ．
  組卷：542引用：9難度：0.8

  解析

• 5．實數-64的立方根是

  ．
  組卷：248引用：6難度：0.7

  解析

• 6．一元二次方程x（x-5）=0的根為

  ．
  組卷：220引用：2難度：0.7

  解析

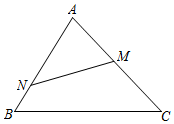• 7．如圖，已知△ABC∽△AMN，點M是AC的中點，AB=6，AC=8，則AN=

  ．
  組卷：1595引用：9難度：0.7

  解析

• 8．請寫出一個圖象經過點（1，3）的一次函數表達式

  ．
  組卷：50引用：2難度：0.7

  解析

• 9．為了落實“雙減”政策，武漢市某學校對初中學生的課外作業時長進行了問卷調查，15名同學的作業時長統計如下表，則這組數據的眾數是

  分鐘．
  

  作業時長（單位：分鐘）	50	60	70	80	90
  人數（單位：人）	2	4	6	2	1
  組卷：96引用：4難度：0.7

  解析

三.解答題（共10小題，共78分）

• 27．在學習了“中心對稱圖形…平行四邊形”這一章后，同學小明對特殊四邊形的探究產生了濃厚的興趣，他發現除了已經學過的特殊四邊形外，還有很多比較特殊的四邊形，勇于創新的他大膽地作出這樣的定義：有一個內角是直角，且對角線互相垂直的四邊形稱為“雙直四邊形”．請你根據以上定義，回答下列問題：
  
  （1）下列關于“雙直四邊形”的說法，正確的有

  （把所有正確的序號都填上）；
  ①雙直四邊形”的對角線不可能相等：
  ②“雙直四邊形”的面積等于對角線乘積的一半；
  ③若一個“雙直四邊形”是中心對稱圖形，則其一定是正方形．
  （2）如圖①，正方形ABCD中，點E、F分別在邊AB、AD上，連接CE，BF，EF，CF，若AE=DF，證明：四邊形BCFE為“雙直四邊形”；
  （3）如圖②，在平面直角坐標系中，已知點A（0，6），C（8，0），點B在線段OC上且AB=BC，是否存在點D在第一象限，使得四邊形ABCD為“雙直四邊形”，若存在；求出所有點D的坐標，若不存在，請說明理由．
  組卷：493引用：5難度：0.3

  解析

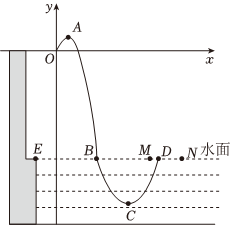• 28．如圖，某跳水運動員進行10米跳臺跳水訓練，水面邊緣點E的坐標為（-

  3

  2

  ，-10），運動員（將運動員看成一點）在空中運動的路線是經過原點O的拋物線，在跳某個規定動作時，運動員在空中最高處A點的坐標為（1，

  5

  4

  ），正常情況下，運動員在距水面高度5米以前．
  必須完成規定的翻騰，打開動作，并調整好入水姿勢，否則就會失誤，運動員入水后，運動路線為另一條拋物線．
  （1）求運動員在空中運動時對應拋物線的解析式并求出入水處B點的坐標；
  （2）若運動員在空中調整好入水姿勢時，恰好距點E的水平距離為5米，問該運動員此次跳水會不會失誤？通過計算說明理由；
  （3）在該運動員入水點的正前方有M，N兩點，且EM=

  21

  2

  ，EN=

  27

  2

  ，該運動員入水后運動路線對應的拋物線解析式為y=a（x-h）²+k,且頂點C距水面4米，若該運動員出水點D在MN之間（包括M，N兩點），求a的取值范圍．
  ?
  組卷：510引用：2難度：0.5

  解析