2023年天津市濱海新區十二校聯考塘沽一中等高考數學模擬試卷（一）

一、選擇題：在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．設全集U={-2，-1，0，1，2，3}，集合A={-1，2}，B={x|x²-4x+3=0}，則?_U（A∪B）=（　　）

  A．{1，3}

  B．{0，3}

  C．{-2，1}

  D．{-2，0}
  組卷：3757引用：31難度：0.8

  解析

• 2．非零向量

  a

  ,

  b

  滿足

  |

  b

  |

  =

  4

  ，

  |

  a

  |

  =

  2

  且

  b

  與

  a

  夾角為θ，則“

  |

  b

  -

  a

  |

  =

  2

  3

  ”是“

  θ

  =

  π

  3

  ”的（　　）

  A．必要而不充分條件	B．充分而不必要條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：434引用：4難度：0.7

  解析

• 3．函數f（x）=

  2

  ln

  |

  x

  |

  x

  的部分圖象大致為（　　）

  A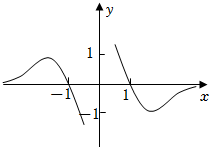．	B．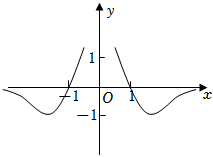
  C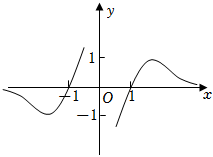．	D．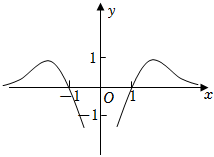
  組卷：575引用：10難度：0.7

  解析

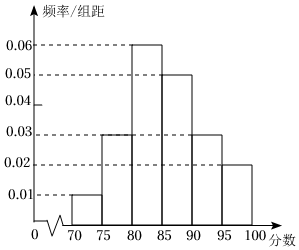• 4．為落實黨中央的“三農”政策，某市組織該市所有鄉鎮干部進行了一期“三農”政策專題培訓，并在培訓結束時進行了結業考試．如圖是該次考試成績隨機抽樣樣本的頻率分布直方圖．則下列關于這次考試成績的估計錯誤的是（　　）

  A．眾數為82.5

  B．中位數為85

  C．平均數為86

  D．有一半以上干部的成績在80～90分之間
  組卷：771引用：7難度：0.7

  解析

• 5．設

  a

  =

  （

  3

  4

  ）

  0

  .

  5

  ，

  b

  =

  （

  4

  3

  ）

  0

  .

  5

  ，

  c

  =

  lo

  g

  3

  4

  （

  lo

  g

  3

  4

  ）

  ，則（　　）

  A．c＜b＜a

  B．c＜a＜b

  C．a＜b＜c

  D．a＜c＜b
  組卷：496引用：9難度：0.7

  解析

• 6．已知正數x,y,z,滿足3^x=4^y=6^z，則下列說法不正確的是（　　）

  A． 1 x + 1 2 y = 1 z	B．3x＞4y＞6z
  C． x + y ＞ （ 3 2 + 2 ） z	D．xy＞2z2
  組卷：681引用：2難度：0.5

  解析

三、解答題：本大題共5小題，共75分.解答應寫出文字說明，證明過程或演算步驟.

• 19．橢圓C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右焦點分別是F₁、F₂，離心率為

  1

  2

  ，過F₁且垂直于x軸的直線被橢圓C截得的線段長為3．
  （Ⅰ）求橢圓C的方程；
  （Ⅱ）已知點H（0，1），若直線y=x+t與橢圓C相交于兩點C，D且直線HC，HD的斜率之和為-2，求實數t的值．
  （Ⅲ）點P是橢圓C上除長軸端點外的任一點，連接PF₁、PF₂，設∠F₁PF₂的角平分線PM交C的長軸于點M（m,0），求m的取值范圍．
  組卷：611引用：3難度：0.5

  解析

• 20．已知函數f（x）=（x-a）lnx-xlna,其中a＞0．
  （1）求f（x）的極值；
  （2）設函數g（x）=f（x）+f（

  1

  x

  ）有三個不同的極值點x₁，x₂，x₃．
  （ⅰ）求實數a的取值范圍；
  （ⅱ）證明：x₁²+x₂²+x₃²＞3．
  組卷：711引用：2難度：0.1

  解析