當前位置：試卷中心 > 試卷詳情

2023年陜西省西安市雁塔區曲江一中中考數學七模試卷

發布：2024/5/2 8:0:9

一、選擇題（本大題共8小題，每小題3分，共24分，在每小題給出的四個選項中，只有一項是符合題目要求的）

1．函數y=
4
-
x
中自變量x的取值范圍是（　　）
A．x＞4 B．x＜4 C．x≥4 D．x≤4
組卷：1068引用：18難度：0.7
解析
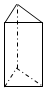2．如圖所示是一個三棱柱，畫出它的主視圖和左視圖均正確的是（　　）
A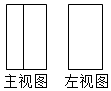． B． C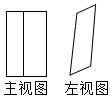． D．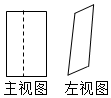
組卷：446引用：26難度：0.6
解析
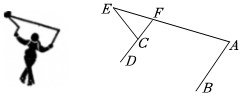3．某學校將國家非物質文化遺產——“抖空竹”引入陽光特色大課間，某同學“抖空竹”的一個瞬間如圖所示，若將左圖抽象成右圖的數學問題：在平面內，AB∥CD，DC的延長線交AE于點F；若∠BAE=75°，∠AEC=35°，則∠DCE的度數為（　　）
A．120° B．115° C．110° D．75°
組卷：322引用：9難度：0.8
解析
4．下列運算正確的是（　　）
A．（-a）²=a² B．a⁶-a²=a⁴
C．-3a²+6a²=3a⁴ D．（a²）³=a⁵
組卷：110引用：4難度：0.9
解析
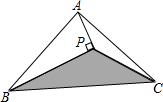5．如圖，△ABC的面積為8cm²，AP垂直∠B的平分線BP于P，則△PBC的面積為（　　）
A．2cm² B．3cm² C．4cm² D．5cm²
組卷：2849引用：18難度：0.7
解析
6．如圖，直線
y
=
-
3
2
x
+
3
與x軸、y軸分別交于A、B兩點，下列各點向右平移2個單位后落在△AOB內部的是（　　）
A．（-2，2） B．
（
-
1
，
3
2
）
C．（0，1） D．（-1，1）
組卷：129引用：2難度：0.5
解析
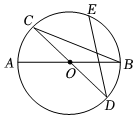7．如圖，AB，CD是⊙O的兩條直徑，E是劣弧
?
BC
的中點，連接BC，DE．若∠ABC=22°，則∠CDE的度數為（　　）
A．22° B．32° C．34° D．44°
組卷：3474引用：24難度：0.7
解析
8．在平面直角坐標系中將拋物線y=ax²-4ax+4a-4沿y軸平移后的頂點恰好落在了x軸上，則正確的平移方式為（　　）
A．將拋物線向上平移2個單位
B．將拋物線向下平移2個單位
C．將拋物線向上平移4個單位
D．將拋物線向下平移4個單位
組卷：213引用：2難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（本大題共13小題，計81分，解答應寫出過程）

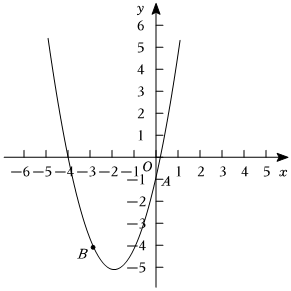25．平面直角坐標系中，已知拋物線
L
1
：
y
=
x
2
+
bx
+
c
過A（0，-1）、B（-3，-4）兩點．
（1）求該拋物線L₁的函數表達式；
（2）將該拋物線L₁向右平移2個單位得到拋物線L₂，點C是拋物線L₂與原拋物線L₁的對稱軸的交點，點D為拋物線L₂對稱軸上的一點，在平面直角坐標系中是否存在點E，使以點B，C，D，E為頂點的四邊形是以BC為邊的菱形，若存在，請求出符合條件的點E的坐標；若不存在，請說明理由．
組卷：250引用：1難度：0.3
解析
26．問題探究：
（1）如圖①，在△ABC中，∠A=45°，AB=3，
AC
=
2
2
，則△ABC的面積為
．
（2）如圖②，△ABC內接于半徑為5的⊙O，若∠C=60°，求AB的長度；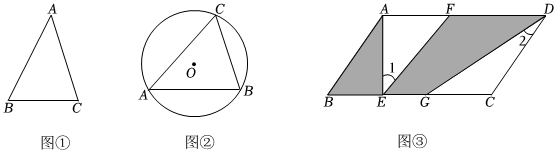

問題解決：
（3）如圖③，某幼兒園有一塊平行四邊形ABCD的空地，其中AB=6米，BC=10米，∠B=60°，為了豐富孩子們的課業生活，將該平行四邊形空地改造成多功能區域，已知點E、G在邊BC上，點F在邊AD上，連接AE，EF，DG．現要求將其中的陰影三角形ABE區域設置成木工區，陰影四邊形EFDG區域設置成益智區，其余區域為角色游戲區．若AB∥EF，∠1+∠2=60°．請問：是否存在一種規劃方案，使得木工區域和益智區域的面積和盡可能大？若存在，求出兩個區域（即兩部分陰影區域）面積和的最大值；若不存在，請說明理由．
組卷：185引用：1難度：0.2
解析