當前位置：試卷中心 > 試卷詳情

2022-2023學年黑龍江省大慶市林甸縣世紀陽光學校七年級（上）期中數學試卷

發布：2024/8/21 0:0:1

一、選擇題（每題3分，共30分）

1．下列各選項中的圖形，繞虛線旋轉一周，所得的幾何體是圓錐的是（　　）
A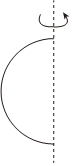． B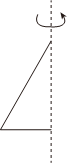． C． D．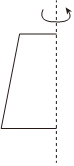
組卷：736引用：14難度：0.8
解析
2．手機移動支付給生活帶來便捷，若張阿姨微信收入5元表示為+5元，則張阿姨微信支出3元應表示為（　　）
A．-3元 B．+3元 C．-8元 D．+2元
組卷：343引用：13難度：0.9
解析
3．一本筆記本的原價為a元，降價后每本比原來便宜了b元，小明買了4本這樣的筆記本，則他一共花費了（　　）
A．（4a-4b）元 B．（4a-b）元 C．（a-4b）元 D．4b元
組卷：147引用：5難度：0.5
解析
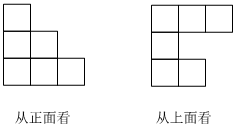4．用小立方塊搭一個幾何體，使得其兩個方向的視圖如圖所示．它最少需要______個小立方塊，最多需要______個小立方塊．（　　）
A．9；14 B．9；16 C．8；16 D．10；14
組卷：298引用：4難度：0.6
解析
5．當x=1時，代數式px³+qx+1的值為2022，則當x=-1時，代數式px³+qx+1的值為（　　）
A．-2019 B．-2020 C．-2021 D．-2022
組卷：1497引用：11難度：0.6
解析
6．有理數m、n在數軸上的位置如圖，則下列關系式正確的個數有（　　）
①m+n＜0；②n-m＞0；③2m-n＞0；④-n-m＞0；⑤
1
m
＞
-
1
n
．
A．1個 B．2個 C．3個 D．4個
組卷：129引用：5難度：0.5
解析
7．定義一種新運算：a*b=ab-b.例如：1*2=1×2-2=0．則（-4）*[2*（-3）]的值為（　　）
A．-3 B．9 C．15 D．27
組卷：519引用：12難度：0.6
解析
8．已知a、b、c均為不等于0的有理數，則
|
a
|
a
+
|
b
|
b
+
|
c
|
c
的值為（　　）
A．1或3 B．-1或-3 C．±1或±3 D．0或3
組卷：99引用：4難度：0.7
解析
9．在求1+6+6²+6³+6⁴+6⁵+6⁶+6⁷+6⁸+6⁹的值時，小林發現：從第二個加數起每一個加數都是前一個加數的6倍，于是她設：
S=1+6+6²+6³+6⁴+6⁵+6⁶+6⁷+6⁸+6⁹①，
然后在①式的兩邊都乘以6，得：
6S=6+6²+6³+6⁴+6⁵+6⁶+6⁷+6⁸+6⁹+6¹⁰②，
②-①得6S-S=6¹⁰-1，即5S=6¹⁰-1，所以S=
6
10
-
1
5
，得出答案后，愛動腦筋的小林想：
如果把“6”換成字母“a”（a≠0且a≠1），能否求出1+a+a²+a³+a⁴+…+a²⁰¹⁷的值？你的答案是（　　）
A．
a
2017
-
1
a
-
1
B．
a
2018
-
1
a
-
1
C．
a
2017
-
1
a
D．a²⁰¹⁷-1
組卷：36引用：1難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題（共50分）

27．請先閱讀下列一組內容，然后解答問題：
∵
1
1
×
2
=
1
-
1
2
，
1
2
×
3
=
1
2
-
1
3
，
1
3
×
4
=
1
3
-
1
4
…
1
9
×
10
=
1
9
-
1
10
，
∴
1
1
×
2
+
1
2
×
3
+
1
3
×
4
+
…
+
1
9
×
10

=
（
1
-
1
2
）
+
（
1
2
-
1
3
）
+
（
1
3
-
1
4
）
+
…
+
（
1
9
-
1
10
）

=
1
-
1
2
+
1
2
-
1
3
+
1
3
-
1
4
+
…
+
1
9
-
1
10
=
1
-
1
10
=
9
10
．
計算：
（1）
1
1
×
2
+
1
2
×
3
+
1
3
×
4
+
1
4
×
5
+
…
+
1
99
×
100
；
（2）已知|a-1|與|b-2|互為相反數，求：
1
ab
+
1
（
a
+
1
）
（
b
+
1
）
+
1
（
a
+
2
）
（
b
+
2
）
+
1
（
a
+
3
）
（
b
+
3
）
+
…
+
1
（
a
+
2019
）
（
b
+
2019
）
．
（3）
1
1
×
3
+
1
3
×
5
+
1
5
×
7
+
…
+
1
99
×
101
．
組卷：490引用：3難度：0.5
解析
28．【問題提出】|a-1|+|a-2|+|a-3|+…+|a-2021|的最小值是多少？
【閱讀理解】
為了解決這個問題，我們先從最簡單的情況入手．|a|的幾何意義是a這個數在數軸上對應的點到原點的距離，那么|a-1|可以看作a這個數在數軸上對應的點到1的距離；|a-1|+|a-2|就可以看作a這個數在數軸上對應的點到1和2兩個點的距離之和．下面我們結合數軸研究|a-1|+|a-2|的最小值．
我們先看a表示的點可能的3種情況，如圖所示：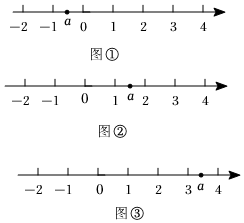

（1）如圖①，a在1的左邊，從圖中很明顯可以看出a到1和2的距離之和大于1．
（2）如圖②，a在1，2之間（包括在1，2上），可以看出a到1和2的距離之和等于1．
（3）如圖③，a在2的右邊，從圖中很明顯可以看出a到1和2的距離之和大于1．
因此，我們可以得出結論：當a在1，2之間（包括在1，2上）時，|a-1|+|a-2|有最小值1．
【問題解決】
（1）|a-4|+|a-7|的幾何意義是
，請你結合數軸探究：|a-4|+|a-7|的最小值是
．
（2）請你結合圖④探究|a-1|+|a-2|+|a-3|的最小值是
，由此可以得出a為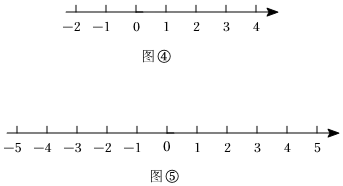
．

（3）|a-1|+|a-2|+|a-3|+|a-4|+|a-5|的最小值為
．
（4）|a-1|+|a-2|+|a-3|+…+|a-2021|的最小值為
．
【拓展應用】如圖，已知a使到-1，2的距離之和小于4，請直接寫出a的取值范圍是
．
組卷：264引用：3難度：0.4
解析