2022-2023學年北京理工大學附中高二(上)期中數學試卷
發布:2024/4/20 14:35:0
一、選擇題共10小題,每小題4分,共40分.在每小題列出的四個選項中,選出符合題目要求的一項.
-
1.直線
x-y+1=0的傾斜角的大小為( )3A.30° B.60° C.120° D.150° 組卷:224引用:19難度:0.9 -
2.已知i是虛數單位,則
=( )1+i1-iA.1 B.-1 C.i D.-i 組卷:77引用:3難度:0.9 -
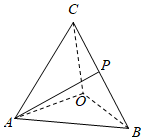 3.在四面體O-ABC中,點P為棱BC的中點.設,OA=a,OB=b,那么向量OC=c用基底{AP,a,b}可表示為( )c
3.在四面體O-ABC中,點P為棱BC的中點.設,OA=a,OB=b,那么向量OC=c用基底{AP,a,b}可表示為( )cA. -12a+12b+12cB. -a+12b+12cC. a+12b+12cD. 12a+12b+12c組卷:408引用:16難度:0.9 -
4.在平面直角坐標系xOy中,半徑為2且過原點的圓的方程可以是( )
A.(x-1)2+(y-1)2=2 B. (x+1)2+(y+2)2=2C.(x-1)2+(y+1)2=4 D.(x-2)2+y2=4 組卷:481引用:2難度:0.7 -
5.已知直線l的方程為x-my+2=0,則直線l( )
A.恒過點(-2,0)且不垂直x軸 B.恒過點(-2,0)且不垂直y軸 C.恒過點(2,0)且不垂直x軸 D.恒過點(2,0)且不垂直y軸 組卷:237引用:3難度:0.5 -
6.已知點P是正方體ABCD-A1B1C1D1的棱A1D1上的一個動點,設異面直線AB與CP所成的角為α,則cosα的最小值是( )
A. 33B. 23C. 255D. 55組卷:121引用:2難度:0.6
三、解答題共4小題,共40分.解答應寫出文字說明、演算步驟或證明過程.
-
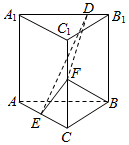 18.已知直三棱柱ABC-A1B1C1中,側面AA1B1B為正方形,AB=BC=2,E,F分別為AC,CC1的中點,D為棱A1B1上的點,BF⊥A1B1.
18.已知直三棱柱ABC-A1B1C1中,側面AA1B1B為正方形,AB=BC=2,E,F分別為AC,CC1的中點,D為棱A1B1上的點,BF⊥A1B1.
(1)求證:AB⊥BC;
(2)若D為棱A1B1的中點,求點A1到平面DFE的距離;
(3)當B1D為何值時,平面BB1C1C與平面DFE所成二面角(銳角)最小?組卷:123引用:2難度:0.4 -
19.在平面直角坐標系xOy中,二次函數f(x)=x2+ax+b(a,b∈R,b>0)的圖像與x軸交于A、B兩點,與y軸交于C點,經過A、B、C三個點的圓記為⊙M.
(1)當a=4,b=2時,求三角形ABC的面積;
(2)求⊙M的方程;
(3)問⊙M是否經過定點(其坐標與a,b的值無關)?請證明你的結論.組卷:33引用:1難度:0.5


