2023-2024學年江蘇省鹽城市東臺中學高三（上）第一次段考數學試卷

一、單項選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知U=R，A={x|-1＜x＜3}，B={x|x≤2}，則?_U（A∪B）=（　　）

  A．（-∞，-1]∪（2，+∞）	B．（-∞，-1）∪[2，+∞）
  C．[3，+∞）	D．（3，+∞）
  組卷：444引用：10難度：0.8

  解析

• 2．設命題p：?n∈N，n²＜3n+4，則p的否定為（　　）

  A．?n∈N，n2＞3n+4	B．?n∈N，n2≤3n+4
  C．?n∈N，n2≥3n+4	D．?n∈N，n2＞3n+4
  組卷：258引用：12難度：0.8

  解析

• 3．已知a,b∈R，則“a＞b＞2”是“a-2＞|b-2|”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：200引用：4難度：0.7

  解析

• 4．設

  a

  =

  1

  2

  ，

  b

  =

  sin

  1

  2

  ，

  c

  =

  lo

  g

  2

  3

  ，則（　　）

  A．a＜b＜c

  B．a＜c＜b

  C．b＜a＜c

  D．b＜c＜a
  組卷：112引用：3難度：0.8

  解析

• 5．函數y=（2^x-2^-x）cosx在區間[-2，2]上的圖象大致為（　　）

  A．	B．
  C．	D．
  組卷：137引用：13難度：0.7

  解析

• 6．牛頓曾經提出了常溫環境下的溫度冷卻模型：

  θ

  =

  （

  θ

  1

  -

  θ

  0

  ）

  e

  -

  kt

  +

  θ

  0

  ，其中t為時間（單位：min），θ₀為環境溫度，θ₁為物體初始溫度，θ為冷卻后溫度．假設在室內溫度為20°C的情況下，一杯飲料由100°C降低到60°C需要20min,則此飲料從60°C降低到40°C需要（　　）

  A．10min

  B．20min

  C．40min

  D．30min
  組卷：242引用：5難度：0.5

  解析

• 7．設函數f（x）=3^x+b,函數f（x）的圖像經過第一、三、四象限，則g（b）=f（b）-f（b-1）的取值范圍為（　　）

  A． （ 0 ， 2 9 ）

  B． （ - ∞ ， 2 9 ）

  C． （ - ∞ ， 2 3 ）

  D． （ 0 ， 2 3 ）
  組卷：280引用：4難度：0.7

  解析

四、解答題：本大題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

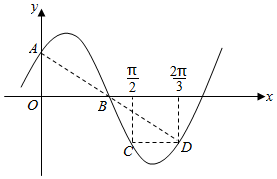• 21．如圖，已知函數f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π），點A，B分別是f（x）的圖象與y軸、x軸的交點，C，D分別是f（x）的圖象上橫坐標為

  π

  2

  、

  2

  π

  3

  的兩點，CD∥x軸，A，B，D共線．
  （Ⅰ）求ω，φ的值；
  （Ⅱ）若關于x的方程f（x）=k+sin2x在區間[

  π

  12

  ，

  π

  2

  ]上恰有唯一實根，求實數k的取值范圍．
  組卷：872引用：3難度：0.1

  解析

• 22．已知函數f（x）=

  - ln （ 1 - | x + 1 | ） ，- 2 ＜ x ＜ 0

  | lnx | ， x ＞ 0

  ．
  （1）求函數f（x）的單調遞增區間；
  （2）若關于x的方程f（2x-1）=m有4個不同的解，記為x₁，x₂，x₃，x₄（x₁＜x₂＜x₃＜x₄），且λ?

  x

  3

  x

  4

  -x₁x₂＞

  1

  5

  恒成立，求λ的取值范圍．
  組卷：127引用：3難度：0.3

  解析