人教A版必修2《全冊綜合驗收評價》2022年同步練習卷

一、選擇題（共8小題，每小題5分，滿分40分）

• 1．已知平面向量

  a

  =（1，1），

  b

  =（1，-1），則向量

  1

  2

  a

  -

  3

  2

  b

  =（　　）

  A．（-2，-1）

  B．（-2，1）

  C．（-1，0）

  D．（-1，2）
  組卷：668引用：19難度：0.9

  解析

• 2．某學校有老師200人，男學生1200人，女學生1000人，現用分層抽樣的方法從全體師生中抽取一個容量為n的樣本，已知女學生一共抽取了80人，則n的值是（　　）

  A．193

  B．192

  C．191

  D．190
  組卷：664引用：11難度：0.9

  解析

• 3．已知復數z滿足（z-1）i=1+i,則z=（　　）

  A．-2-i

  B．-2+i

  C．2-i

  D．2+i
  組卷：3040引用：45難度：0.9

  解析

• 4．已知向量

  a

  與

  b

  的夾角為30°，且|

  a

  |=1，|2

  a

  -

  b

  |=1，則|

  b

  |=（　　）

  A． 6

  B． 5

  C． 3

  D． 2
  組卷：82引用：2難度：0.8

  解析

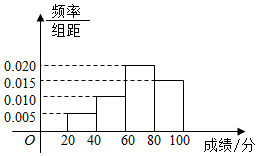• 5．某學校組織學生參加英語測試，成績的頻率分布直方圖如圖，數據的分組依次為[20，40），[40，60），[60，80），[80，100]，若低于60分的人數是15人，則該班的學生人數是（　　）

  A．45

  B．50

  C．55

  D．60
  組卷：773引用：56難度：0.9

  解析

• 6．已知圓錐的表面積等于12πcm²，其側面展開圖是一個半圓，則底面圓的半徑為（　　）

  A．1cm

  B．2cm

  C．3cm

  D． 3 2 cm
  組卷：460引用：13難度：0.7

  解析

• 7．已知向量

  a

  =（cosθ-2，sinθ），其中θ∈R，則|

  a

  |的最小值為（　　）

  A．1

  B．2

  C． 5

  D．3
  組卷：113引用：5難度：0.6

  解析

四、解答題（本大題共6小題，共70分）

• 21．交通指數是指交通擁堵指數的簡稱，是綜合反映道路網暢通或擁堵的概念性指數值，記交通指數為T，其范圍為[0，10]，分別有五個級別：T∈[0，2），暢通；T∈[2，4），基本暢通；T∈[4，6），輕度擁堵；T∈[6，8），中度擁堵；T∈[8，10]，嚴重擁堵．在晚高峰時段（T≥2），從某市交通指揮中心選取了市區20個交通路段，依據其交通指數數據繪制的頻率分布直方圖如圖所示．
  （1）求出輕度擁堵、中度擁堵、嚴重擁堵的路段的個數；
  （2）用分層抽樣的方法從輕度擁堵、中度擁堵、嚴重擁堵的路段中共抽取6個路段，求依次抽取的三個級別路段的個數；
  （3）從（2）中抽取的6個路段中任取2個，求至少有1個路段為輕度擁堵的概率．
  組卷：32引用：1難度：0.7

  解析

• 22．如圖，在正三棱柱ABC-A₁B₁C₁中，AB=2，AA₁=2，由頂點B沿棱柱側面經過棱AA₁到頂點C₁的最短路線與AA₁的交點記為M，求：
  （Ⅰ）三棱柱的側面展開圖的對角線長；
  （Ⅱ）該最短路線的長及

  A

  1

  M

  AM

  的值；
  （Ⅲ）平面C₁MB與平面ABC所成二面角（銳角）的大小．
  組卷：350引用：5難度：0.7

  解析