2022-2023學年湖北省荊荊宜三校高三(上)聯考數學試卷(9月份)
發布:2024/4/20 14:35:0
一、選擇題:本大題共8小題,每一小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.已知集合
,則A∪B=( )A={x|x2-x-2≤0},B={x|y=x-1}A.[1,2] B.[-1,+∞) C.[-1,1] D.[1,+∞) 組卷:30引用:1難度:0.7 -
2.已知角θ的終邊經過點
,則角θ可以為( )P(32,-12)A. 5π6B. 2π3C. 11π6D. 5π3組卷:357引用:3難度:0.7 -
3.已知A,B為兩個隨機事件,P(A),P(B)>0,則“A,B相互獨立”是“
”的( )P(A|B)=P(A|B)A.充分不必要條件 B.必要不充分條件 C.充分必要條件 D.既不充分也不必要條件 組卷:410引用:3難度:0.6 -
4.衡量曲線彎曲程度的重要指標是曲率,曲線的曲率定義如下:若f'(x)是f(x)的導函數,f″(x)是f'(x)的導函數,則曲線y=f(x)在點(x,f(x))處的曲率
已知f(x)=lnx-cos(x-1),則曲線y=f(x)在點(1,f(1))處的曲率為( )K=|f″(x)|(1+[f′(x)]2)32?A.0 B. 24C. 22D. 2組卷:104引用:4難度:0.8 -
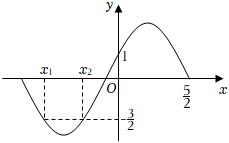 5.已知函數的部分圖象如圖,f(x1)=f(x2)=-f(x)=2sin(ωx+φ)(ω>0,0<φ<π2),則32=( )cos[π6(x2-x1)]
5.已知函數的部分圖象如圖,f(x1)=f(x2)=-f(x)=2sin(ωx+φ)(ω>0,0<φ<π2),則32=( )cos[π6(x2-x1)]A. -34B. -74C. 34D. 74組卷:173引用:3難度:0.6 -
6.已知(mx+1)n(n∈N*,m∈R)的展開式只有第5項的二項式系數最大,設(mx+1)n=a0+a1x+a2x2+…+anxn,若a1=8,則a2+a3+?+an=( )
A.63 B.64 C.247 D.255 組卷:306引用:4難度:0.6 -
7.已知tanα,tanβ是方程ax2+bx+c=0(a≠0)的兩根,有以下四個命題:
甲:;tan(α+β)=-12
乙:tanαtanβ=7:3;
丙:;sin(α+β)cos(α-β)=54
丁:tanαtanβtan(α+β)-tan(α+β)=5:3.
如果其中只有一個假命題,則該命題是( )A.甲 B.乙 C.丙 D.丁 組卷:142引用:6難度:0.4
四、解答題:本大題共6小題,共70分.解答應寫出文字說明、證明過程或演算步驟.
-
21.設橢圓
是橢圓Γ的左、右焦點,點Γ:x2a2+y2b2=1(a>b>0),F1,F2在橢圓Γ上,點P(4,0)在橢圓Γ外,且A(1,32).|PF2|=4-3
(1)求橢圓Γ的方程;
(2)若,點C為橢圓Γ上橫坐標大于1的一點,過點C的直線l與橢圓有且僅有一個交點,并與直線PA,PB交于M,N兩點,O為坐標原點,記△OMN,△PMN的面積分別為S1,S2,求B(1,-32)的最小值.S21-S1S2+S22組卷:167引用:2難度:0.6 -
22.已知函數f(x)=xln(x+1)+x-ex+1.
(1)討論函數f(x)的零點個數;
(2)記f(x)較大的零點為x0,求證:.ex02+1<4ln(x0+1)x0<2ex02組卷:47引用:1難度:0.4


