人教五四新版八年級(下)中考題單元試卷:第25章 平行四邊形(04)
發布:2024/11/7 16:30:6
一、選擇題(共5小題)
-
1.已知四邊形ABCD,下列說法正確的是( )
A.當AD=BC,AB∥DC時,四邊形ABCD是平行四邊形 B.當AD=BC,AB=DC時,四邊形ABCD是平行四邊形 C.當AC=BD,AC平分BD時,四邊形ABCD是矩形 D.當AC=BD,AC⊥BD時,四邊形ABCD是正方形 組卷:4575引用:83難度:0.9 -
 2.如圖,在平行四邊形ABCD中,AB>BC,按以下步驟作圖:以A為圓心,小于AD的長為半徑畫弧,分別交AB、CD于E、F;再分別以E、F為圓心,大于EF的長半徑畫弧,兩弧交于點G;作射線AG交CD于點H.則下列結論:12
2.如圖,在平行四邊形ABCD中,AB>BC,按以下步驟作圖:以A為圓心,小于AD的長為半徑畫弧,分別交AB、CD于E、F;再分別以E、F為圓心,大于EF的長半徑畫弧,兩弧交于點G;作射線AG交CD于點H.則下列結論:12
①AG平分∠DAB,②CH=DH,③△ADH是等腰三角形,④S△ADH=12S四邊形ABCH.12
其中正確的有( )A.①②③ B.①③④ C.②④ D.①③ 組卷:743引用:71難度:0.7 -
3.已知點A(0,0),B(0,4),C(3,t+4),D(3,t).記N(t)為?ABCD內部(不含邊界)整點的個數,其中整點是指橫坐標和縱坐標都是整數的點,則N(t)所有可能的值為( )
A.6、7 B.7、8 C.6、7、8 D.6、8、9 組卷:1805引用:82難度:0.7 -
 4.如圖,在Rt△ABC中,∠B=90°,AB=3,BC=4,點D在BC上,以AC為對角線的所有?ADCE中,DE最小的值是( )
4.如圖,在Rt△ABC中,∠B=90°,AB=3,BC=4,點D在BC上,以AC為對角線的所有?ADCE中,DE最小的值是( )A.2 B.3 C.4 D.5 組卷:5491引用:97難度:0.9 -
 5.如圖,平行四邊形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中點,過D分別作DP⊥AF于P,DQ⊥CE于Q,則DP:DQ等于( )
5.如圖,平行四邊形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中點,過D分別作DP⊥AF于P,DQ⊥CE于Q,則DP:DQ等于( )A.3:4 B. :2135C. :2136D.2 :313組卷:3686引用:79難度:0.3
二、填空題(共8小題)
-
 6.如圖,分別以Rt△ABC的直角邊AC及斜邊AB為邊向外作等邊△ACD、等邊△ABE,EF⊥AB,垂足為F,連接DF,當=ACAB時,四邊形ADFE是平行四邊形.組卷:3132引用:67難度:0.9
6.如圖,分別以Rt△ABC的直角邊AC及斜邊AB為邊向外作等邊△ACD、等邊△ABE,EF⊥AB,垂足為F,連接DF,當=ACAB時,四邊形ADFE是平行四邊形.組卷:3132引用:67難度:0.9 -
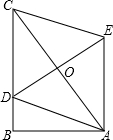
 7.如圖,四邊形ABCD的對角線相交于點O,AO=CO,請添加一個條件 (只添一個即可),使四邊形ABCD是平行四邊形.組卷:2766引用:74難度:0.7
7.如圖,四邊形ABCD的對角線相交于點O,AO=CO,請添加一個條件 (只添一個即可),使四邊形ABCD是平行四邊形.組卷:2766引用:74難度:0.7 -
 8.如圖,一個平行四邊形的活動框架,對角線是兩根橡皮筋.若改變框架的形狀,則∠α也隨之變化,兩條對角線長度也在發生改變.當∠α為 度時,兩條對角線長度相等.組卷:496引用:84難度:0.7
8.如圖,一個平行四邊形的活動框架,對角線是兩根橡皮筋.若改變框架的形狀,則∠α也隨之變化,兩條對角線長度也在發生改變.當∠α為 度時,兩條對角線長度相等.組卷:496引用:84難度:0.7 -
 9.如圖,P為平行四邊形ABCD邊AD上一點,E、F分別為PB、PC的中點,△PEF、△PDC、△PAB的面積分別為S、S1、S2,若S=2,則S1+S2=.組卷:1782引用:94難度:0.7
9.如圖,P為平行四邊形ABCD邊AD上一點,E、F分別為PB、PC的中點,△PEF、△PDC、△PAB的面積分別為S、S1、S2,若S=2,則S1+S2=.組卷:1782引用:94難度:0.7 -
10.如圖,?ABCD中,對角線AC與BD相交于點E,∠AEB=45°,BD=2,將△ABC沿AC所在直線翻折180°到其原來所在的同一平面內,若點B的落點記為B′,則DB′的長為 .
 組卷:2523引用:96難度:0.7
組卷:2523引用:96難度:0.7
三、解答題(共17小題)
-
 29.已知,如圖,在?ABCD中,AE⊥BC,垂足為E,CE=CD,點F為CE的中點,點G為CD上的一點,連接DF、EG、AG,∠1=∠2.
29.已知,如圖,在?ABCD中,AE⊥BC,垂足為E,CE=CD,點F為CE的中點,點G為CD上的一點,連接DF、EG、AG,∠1=∠2.
(1)若CF=2,AE=3,求BE的長;
(2)求證:∠CEG=∠AGE.12組卷:10180引用:77難度:0.5 -
 30.如圖,在?ABCD中,M、N分別是AD,BC的中點,∠AND=90°,連接CM交DN于點O.
30.如圖,在?ABCD中,M、N分別是AD,BC的中點,∠AND=90°,連接CM交DN于點O.
(1)求證:△ABN≌△CDM;
(2)過點C作CE⊥MN于點E,交DN于點P,若PE=1,∠1=∠2,求AN的長.組卷:5338引用:75難度:0.1


