蘇科新版八年級上冊《第1章 全等三角形》2020年單元測試卷（2）

一、選擇題

• 1．全等形都相同的是（　　）

  A．形狀

  B．大小

  C．邊數和角度

  D．形狀和大小
  組卷：114引用：3難度：0.9

  解析

• 2．下圖中，全等的圖形有（　　）
  

  A．2組

  B．3組

  C．4組

  D．5組
  組卷：363引用：3難度：0.9

  解析

• 3．有以下說法：
  ①△ABC在平移的過程中，對應線段一定相等；
  ②△ABC在平移過程中，對應線段一定平行；
  ③△ABC在平移過程中，周長保持不變；
  ④△ABC在平移過程中，對應邊中點的連線的長度等于平移的距離．
  正確的是（　　）

  A．①②③④

  B．①③④

  C．②③④

  D．①②③
  組卷：334引用：4難度：0.9

  解析

• 4．如圖為6個邊長相等的正方形的組合圖形，則∠1+∠2+∠3=（　　）

  A．90°

  B．135°

  C．150°

  D．180°
  組卷：6115引用：31難度：0.7

  解析

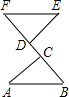• 5．如圖所示，△ABC≌△EFD，那么（　　）

  A．AB=DE，AC=EF，BC=DF	B．AB=DF，AC=DE，BC=EF
  C．AB=EF，AC=DE，BC=DF	D．AB=EF，AC=DF，BC=DE
  組卷：818引用：22難度：0.9

  解析

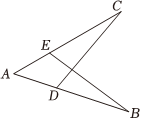• 6．如圖，AB=AC，添加下列條件，能用SAS判斷△ABE≌△ACD的是（　　）

  A．∠B=∠C

  B．∠AEB=∠ADC

  C．AE=AD

  D．BE=DC
  組卷：421引用：6難度：0.9

  解析

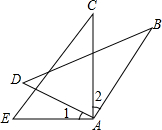• 7．如圖，AB=AC，AD=AE，欲證△ABD≌△ACE，可補充條件（　　）

  A．∠1=∠2

  B．∠B=∠C

  C．∠D=∠E

  D．∠BAE=∠CAD
  組卷：271引用：4難度：0.9

  解析

• 8．如圖，在△ABC中，∠ABC=45°，AC=8cm,F是高AD和BE的交點，則BF的長是（　　）

  A．4cm

  B．6cm

  C．8cm

  D．9cm
  組卷：2242引用：81難度：0.9

  解析

三、解答題

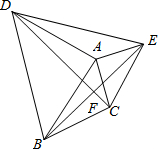• 25．如圖，△ABD和△ACE是兩個等腰直角三角形，AB=AD，AC=AE，∠BAD=∠CAE=90°，CD與BE交于F．
  （1）判斷CD與BE有怎樣的數量關系；
  （2）求∠BFD的度數．
  （3）取BC的中點M，連MA，探討MA與DE的數量和位置關系．
  組卷：250引用：1難度：0.6

  解析

• 26．復習“全等三角形”的知識時，老師布置了一道作業題：
  “如圖①，已知，在△ABC中，AB=AC，P是△ABC中內任意一點，將AP繞點A順時針旋轉至AQ，使∠QAP=∠BAC，連接BQ、CP則BQ=CP．”
  小亮是個愛動腦筋的同學，他通過對圖①的分析，證明了△ABQ≌△ACP，從而證得BQ=CP．之后，他將點P移到等腰三角形ABC外，原題中其它條件不變，發現“BQ=CP”仍然成立，請你就圖②給出證明．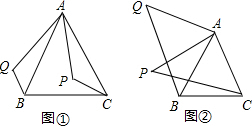
  
  組卷：1039引用：7難度：0.7

  解析