2022-2023學年陜西省西安市黃河中學等高一（下）第二次聯考數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．從全市5萬名高中生中隨機抽取500名學生，以此來了解這5萬名高中生的身高，在這一情境中，這5萬名高中生的身高的全體是指（　　）

  A．個體

  B．總體

  C．樣本

  D．樣本量
  組卷：57引用：5難度：0.7

  解析

• 2．已知集合A={x|x是四棱柱}，B={x|x是長方體}，C={x|x是直四棱柱}，D={x|x是正四棱柱}，集合A，B，C，D之間的關系為（　　）

  A．D?B?C?A

  B．D?C?B?A

  C．B?D?C?A

  D．B?C?D?A
  組卷：147引用：5難度：0.7

  解析

• 3．若復數

  z

  =

  i

  2

  2

  +

  3

  i

  ，則

  z

  =（　　）

  A． 2 13 + 3 13 i

  B． 2 13 - 3 13 i

  C． - 2 13 + 3 13 i

  D． - 2 13 - 3 13 i
  組卷：47引用：4難度：0.8

  解析

• 4．已知向量

  a

  =

  （

  2

  ，-

  1

  ）

  ，點A（1，1），B（m,3），若

  a

  ⊥

  AB

  ，則m=（　　）

  A．3

  B．-3

  C．2

  D．-2
  組卷：79引用：3難度：0.8

  解析

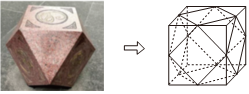• 5．某廣場設置了一些石凳供大家休息，如圖，每個石凳都是由正方體截去八個相同的正三棱錐得到的幾何體，則下列結論不正確的是（　　）

  A．該幾何體的面是等邊三角形或正方形

  B．該幾何體恰有12個面

  C．該幾何體恰有24條棱

  D．該幾何體恰有12個頂點
  組卷：137引用：4難度：0.8

  解析

• 6．已知一組數據x₁，x₂，?，x_n的平均數為

  x

  ，標準差為s,則數據3x₁-1，3x₂-1，?，3x_n-1的平均數和方差分別為（　　）

  A． 3 x - 1 ， 3 s - 1

  B． 3 x ， 3 s

  C． 3 x - 1 ， 9 s 2

  D． 3 x - 1 ， 9 s 2 - 1
  組卷：144引用：9難度：0.8

  解析

• 7．在正方體ABCD-A₁B₁C₁D₁中，E，F，M，N分別是AD，A₁D₁，BC，CC₁的中點，則異面直線EF和MN所成角的弧度數為（　　）

  A． π 6

  B． π 4

  C． π 3

  D． π 2
  組卷：53引用：2難度：0.7

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

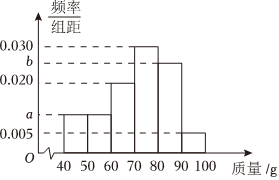• 21．某企業生產某批產品按產品質量（單位：g）從高到低依比例劃定A，B，C，D，E五個等級，A等級優于B等級，B等級優于C等級，C等級優于D等級，D等級優于E等級．其中A等級產品占該批產品的12%，B等級產品占該批產品的32%，C等級產品占該批產品的37%，D等級產品占該批產品的15%，E等級產品占該批產品的4%．現從該批產品中隨機抽取100件產品對其質量進行分析，并繪制出如圖所示的頻率分布直方圖，其中5a=2b.
  （1）求圖中a,b的值；
  （2）根據頻率分布直方圖，估計企業生產的該批產品的質量的平均數（同一組的值用該組區間的中點值作為代表）；
  （3）用樣本估計總體的方法，估計該批產品中C等級及以上等級的產品質量至少為多少g？
  組卷：97引用：3難度：0.5

  解析

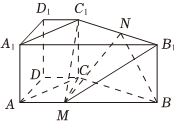• 22．如圖，在直四棱柱ABCD-A₁B₁C₁D₁中，AA₁=2，底面ABCD是直角梯形，AB⊥AD，AB∥CD，AB=4，

  AD

  =

  3

  ，DC=1，點M為AB上一點，且AM=1．
  （1）證明：平面MCC₁⊥平面DCC₁D₁．
  （2）點N是B₁C₁上一點，且MN∥平面ACC₁A₁，求四面體MNBB₁的體積．
  組卷：53引用：5難度：0.5

  解析