2022-2023學年安徽省滁州市定遠縣尚真學校九年級（上）月考數學試卷（12月份）

一、選擇題（本大題共10小題，共40分。在每小題列出的選項中，選出符合題目的一項）

• 1．函數

  y

  =

  （

  m

  -

  3

  ）

  x

  m

  2

  -

  7

  +2020x-2020是關于x的二次函數，則m的值為（　　）

  A．3

  B．0

  C．-3

  D．±3
  組卷：1189引用：16難度：0.7

  解析

• 2．將拋物線y=-3x²平移，得到拋物線y=-3（x-1）²-2，下列平移方式中，正確的是（　　）

  A．先向左平移1個單位，再向上平移2個單位

  B．先向左平移1個單位，再向下平移2個單位

  C．先向右平移1個單位，再向上平移2個單位

  D．先向右平移1個單位，再向下平移2個單位
  組卷：3563引用：68難度：0.7

  解析

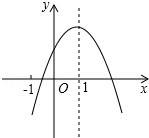• 3．已知二次函數y=ax²+bx+c（a≠0）的圖象如圖，有下列5個結論：①4a+2b+c＞0；②abc＜0；③b＜a-c；④3b＞2c；⑤a+b＜m（am+b），（m≠1的實數）；其中正確結論的個數為（　　）

  A．2個

  B．3個

  C．4個

  D．5個
  組卷：2592引用：5難度：0.5

  解析

• 4．商店銷售一種進價為50元/件的商品，售價為60元/件，每星期可賣出200件，若每件商品的售價上漲1元，則每星期就會少賣10件．每件商品的售價上漲x元（x為正整數），每星期銷售的利潤為y元，則y與x的函數關系式為（　　）

  A．y=10（200-10x）	B．y=200（10+x）
  C．y=10（200-10x）2	D．y=（10+x）（200-10x）
  組卷：1904引用：10難度：0.7

  解析

• 5．二位同學在研究函數y=a（x+3）（x-

  2

  a

  ）（a為實數，且a≠0）時，甲發(fā)現當0＜a＜1時，函數圖象的頂點在第四象限；乙發(fā)現方程a（x+3）（x-

  2

  a

  ）+5=0必有兩個不相等的實數根．則（　　）

  A．甲、乙的結論都錯誤

  B．甲的結論正確，乙的結論錯誤

  C．甲、乙的結論都正確

  D．甲的結論錯誤，乙的結論正確
  組卷：1126引用：5難度：0.7

  解析

• 6．已知拋物線y=-x²-2x+m+1與x軸沒有交點，則函數

  y

  =

  m

  x

  和函數y=mx-m的大致圖象是（　　）

  A．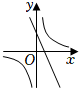

  B．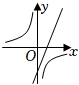

  C．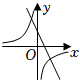

  D．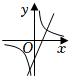
  組卷：131引用：3難度：0.7

  解析

• 7．如圖，A（0，1），B（1，5），曲線BC是雙曲線y=

  k

  x

  （k≠0）的一部分．曲線AB與BC組成圖形G．由點C開始不斷重復圖形G形成一線“波浪線”．若點P（2020，m），Q（x,n）在該“波浪線”上，則m的值為____，n的最大值為____．（　　）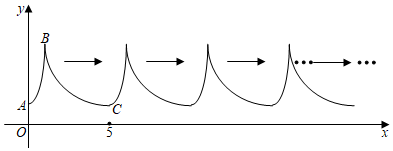
  

  A．m=1，n=1

  B．m=5，n=1

  C．m=1，n=5

  D．m=1，n=4
  組卷：689引用：4難度：0.5

  解析

三、解答題（本大題共9小題，共90分。解答應寫出文字說明，證明過程或演算步驟）

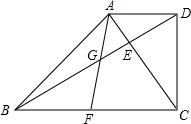• 22．已知，如圖，在梯形ABCD中，AD∥BC，∠BCD=90°，對角線AC、BD相交于點E，且AC⊥BD．
  （1）求證：CD²=BC?AD；
  （2）點F是邊BC上一點，連接AF，與BD相交于點G，如果∠BAF=∠DBF，求證：

  A

  G

  2

  A

  D

  2

  =

  BG

  BD

  ．
  組卷：1674引用：8難度：0.5

  解析

• 23．如圖，二次函數y=ax²+bx+c（a≠0）的圖象交x軸于A，B兩點，交y軸于點D，點B的坐標為（3，0），頂點C的坐標為（1，4）．
  （1）求二次函數的解析式和直線BD的解析式；
  （2）點P是直線BD上的一個動點，過點P作x軸的垂線，交拋物線于點M，當點P在第一象限時，求線段PM長度的最大值；
  （3）在拋物線上是否存在點Q，且點Q在第一象限，使△BDQ中BD邊上的高為

  2

  ？若存在，求出點Q的坐標；若不存在，請說明理由．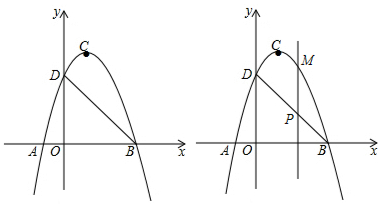
  
  組卷：1169引用：10難度：0.3

  解析