2022-2023學年湖南省長沙市岳麓區長郡梅溪湖中學高二(下)期中數學試卷
發布:2024/11/29 18:30:2
一、選擇題(本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求的。)
-
1.設集合A={y|y=
},B={x|-1≤x≤3},則( )x-x2+6A.A=B B.A?B C.A?B D.A∩B=? 組卷:73引用:1難度:0.9 -
2.已知函數y=f(x)的定義域是[-8,1],則函數g(x)=
的定義域是( )f(2x+1)x+2A.(-∞,-2)∪(-2,3] B.[-8,-2)∪(-2,1] C.[- ,-2)∪(-2,0]92D.[- ,-2]92組卷:5039引用:31難度:0.9 -
3.設函數f(x)的定義域為R,且f(x+2)是奇函數,則f(x)圖像( )
A.關于點(2,0)中心對稱 B.關于點(-2,0)中心對稱 C.關于直線x=2對稱 D.關于直線x=-2對稱 組卷:61引用:1難度:0.8 -
4.如果ξ是離散型隨機變量,η=2ξ+3,則下列結論中正確的是( )
A. ,E(ξ)=E(η)-32D(ξ)=D(η)-32B. ,E(ξ)=E(η)2D(ξ)=D(η)-32C. ,E(ξ)=E(η)-32D(ξ)=D(η)-94D. ,E(ξ)=E(η)-32D(ξ)=D(η)4組卷:120引用:1難度:0.8 -
5.關于“函數
,f(x)=x-13x-14的最大、最小值與函數x∈(-∞,14)∪(14,+∞),x∈Z的最大、最小值”,下列說法中正確的是( )g(x)=x-13x-14A.f(x)有最大、最小值,g(x)有最大、最小值 B.f(x)有最大、最小值,g(x)無最大、最小值 C.f(x)無最大、最小值,g(x)有最大、最小值 D.f(x)無最大、最小值,g(x)無最大、最小值 組卷:123引用:2難度:0.5 -
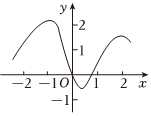 6.如圖是下列某個函數在區間[-2,2]的大致圖象,則該函數是( )
6.如圖是下列某個函數在區間[-2,2]的大致圖象,則該函數是( )A.f(x)= cosx3+3x2-3xx2+1x2B. f(x)=x3+3x2-3xx2+1C. f(x)=x3-x2+xx2+1sinxD. f(x)=x2-5xx2+1cosx組卷:52引用:4難度:0.7 -
7.“
”是“不等式a1x2+b1x+c1>0與a2x2+b2x+c2>0同解”的( )條件.a1a2=b1b2=c1c2A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要 組卷:44引用:2難度:0.6
四、解答題(本題共6小題,共70分.請在指定區域作答,解答時應寫出文字說明、證明過程或演算步驟)
-
21.若函數f(x)在x∈[a,b]時,函數值y的取值區間恰為
,則稱[a,b]為f(x)的一個“倒域區間”.定義在[-2,2]上的奇函數g(x),當x∈[0,2]時,g(x)=-x2+2x.[1b,1a]
(1)求g(x)在[-2,0)上的解析式;
(2)求g(x)的“倒域區間”.組卷:31引用:1難度:0.4 -
22.已知h(x)=sinx,x∈R.
(1)求方程h(x)=ln(x+1)的根的個數;
(2)證明:h(2)+h(4)+h(6)+…+h(2n)>(n∈N*).36-cos(2n+1)2sin1組卷:27引用:1難度:0.3


