當前位置：試卷中心 > 試卷詳情

2023年浙江省杭州市高考數學二模試卷

發布：2024/12/28 11:30:2

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，有一項是符合題目要求的.

1．設集合A={x∈N^*|x²≤4x}，
B
=
{
x
|
y
=
x
-
3
}
，則A∩?_RB=（　　）
A．[0，3] B．[1，3] C．{1，2} D．{1，2，3}
組卷：365引用：7難度：0.8
解析
2．設復數z滿足z（1+i）=-2+i（i是虛數單位），則|z|=（　　）
A．
10
2
B．
5
4
C．
5
2
D．
5
2
組卷：302引用：4難度：0.7
解析
3．在數列{a_n}中，“數列{a_n}是等比數列”是“
a
2
2
=
a
1
a
3
”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：280引用：7難度：0.7
解析
4．已知平面向量
a
=
（
1
，
3
）
，
|
b
|
=
2
，且
|
a
-
b
|
=
10
，則
（
2
a
+
b
）
?
（
a
-
b
）
=（　　）
A．1 B．14 C．
14
D．
10
組卷：900引用：20難度：0.7
解析
5．某興趣小組研究光照時長x（h）和向日葵種子發芽數量y（顆）之間的關系，采集5組數據，作如圖所示的散點圖．若去掉D（10，2）后，下列說法正確的是（　　）
A．相關系數r變小
B．決定系數R²變小
C．殘差平方和變大
D．解釋變量x與預報變量y的相關性變強
組卷：296引用：10難度：0.7
解析
6．已知a＞1，b＞1，且log₂
a
=
lo
g
b
4，則ab的最小值為（　　）
A．4 B．8 C．16 D．32
組卷：1097引用：12難度：0.6
解析
7．如圖，點A，B，C，M，N為正方體的頂點或所在棱的中點，則下列各圖中，不滿足直線MN∥平面ABC的是（　　）
A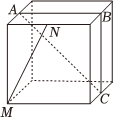． B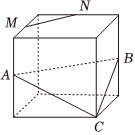． C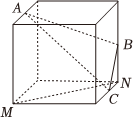． D．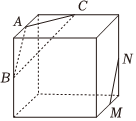
組卷：909引用：10難度：0.5
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題

21．馬爾科夫鏈是概率統計中的一個重要模型，也是機器學習和人工智能的基石，在強化學習、自然語言處理、金融領域、天氣預測等方面都有著極其廣泛的應用．其數學定義為：假設我們的序列狀態是…，X_t-2，X_t-1，X_t，X_t+1，…，那么X_t+1時刻的狀態的條件概率僅依賴前一狀態X_t，即P（X_t+1|…，X_t-2，X_t-1，X_t）=P（X_t+1|X_t）．
現實生活中也存在著許多馬爾科夫鏈，例如著名的賭徒模型．
假如一名賭徒進入賭場參與一個賭博游戲，每一局賭徒賭贏的概率為50%，且每局賭贏可以贏得1元，每一局賭徒賭輸的概率為50%，且賭輸就要輸掉1元．賭徒會一直玩下去，直到遇到如下兩種情況才會結束賭博游戲：一種是手中賭金為0元，即賭徒輸光；一種是賭金達到預期的B元，賭徒停止賭博．記賭徒的本金為A（A∈N^*，A＜B），賭博過程如圖的數軸所示．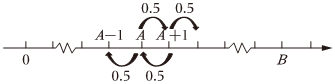

當賭徒手中有n元（0≤n≤B，n∈N）時，最終輸光的概率為P（n），請回答下列問題：
（1）請直接寫出P（0）與P（B）的數值．
（2）證明{P（n）}是一個等差數列，并寫出公差d.
（3）當A=100時，分別計算B=200，B=1000時，P（A）的數值，并結合實際，解釋當B→∞時，P（A）的統計含義．
組卷：1727引用：5難度：0.4
解析
22．已知函數f（x）=e^x-
a
x
（a∈R）．
（1）討論函數f（x）零點個數；
（2）若|f（x）|＞alnx-a恒成立，求a的取值范圍．
組卷：440引用：6難度：0.5
解析