《第3章 空間向量與立體幾何》2009年單元測試卷（東升學校）

一、選擇題（本大題8小題，每小題5分，共40分）

• 1．若

  a

  ，

  b

  ，

  c

  是空間任意三個向量，λ∈R，下列關系式中，不成立的是（　　）

  A． a + b = b + a	B． λ （ a + b ） = λ a + λ b
  C． （ a + b ） + c = a + （ b + c ）	D． b = λ a
  組卷：199引用：5難度：0.9

  解析

• 2．給出下列命題：
  ①已知

  a

  ⊥

  b

  ，則

  a

  ?

  （

  b

  +

  c

  ）

  +

  c

  ?

  （

  b

  -

  a

  ）

  =

  b

  ?

  c

  ；
  ②A、B、M、N為空間四點，若

  BA

  ，

  BM

  ，

  BN

  不構成空間的一個基底，則A、B、M、N共面；
  ③已知

  a

  ⊥

  b

  ，則

  a

  ，

  b

  與任何向量不構成空間的一個基底；
  ④已知

  {

  a

  ，

  b

  ，

  c

  }

  是空間的一個基底，則基向量

  a

  ，

  b

  可以與向量

  m

  =

  a

  +

  c

  構成空間另一個基底．
  正確命題個數是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：99引用：3難度：0.7

  解析

• 3．已知

  a

  與

  b

  均為單位向量，它們的夾角為60°，那么

  |

  a

  +

  3

  b

  |

  =（　　）

  A． 7

  B． 10

  C． 13

  D．4
  組卷：4095引用：58難度：0.9

  解析

• 4．若|

  a

  |=1，|

  b

  |=2，

  c

  =

  a

  +

  b

  ，且

  c

  ⊥

  a

  ，則向量

  a

  與

  b

  的夾角為（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  組卷：610引用：50難度：0.9

  解析

• 5．已知

  a

  =

  （

  -

  3

  ，

  2

  ，

  5

  ）

  ，

  b

  =

  （

  1

  ，

  x

  ,-

  1

  ）

  ，且

  a

  ?

  b

  =2，則x的值為（　　）

  A．3

  B．4

  C．5

  D．6
  組卷：1083引用：15難度：0.9

  解析

• 6．若直線l的方向向量為

  a

  ，平面α的法向量為

  n

  ，能使l∥α的是（　　）

  A． a =（1，0，0）， n =（-2，0，0）

  B． a =（1，3，5）， n =（1，0，1）

  C． a =（0，2，1）， n =（-1，0，-1）

  D． a =（1，-1，3）， n =（0，3，1）
  組卷：1287引用：28難度：0.7

  解析

三、解答題（本大題共6小題，共80分）

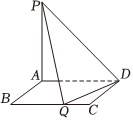• 18．如圖所示，矩形ABCD的邊AB=a,BC=2，PA⊥平面ABCD，PA=2，現有數據：①

  a

  =

  3

  2

  ；②a=1；③

  a

  =

  3

  ；④a=2；⑤a=4．
  （1）當在BC邊上存在點Q，使PQ⊥QD時，a可能取所給數據中的哪些值，請說明理由；
  （2）在滿足（1）的條件下，a取所給數據中的最大值時，求直線PQ與平面ADP所成角的正切值；
  （3）記滿足（1）的條件下的Q點為Q_n（n=1，2，3，…），若a取所給數據的最小值時，這樣的點Q_n有幾個，試求二面角Q_n-PA-Q_n+1的大小．
  組卷：47引用：2難度：0.1

  解析

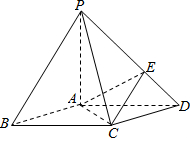• 19．如圖，在底面是菱形的四棱錐P-ABCD中，∠ABC=60°，PA=AC=a,PB=PD=

  2

  a

  ，點E在PD上，且PE：ED=2：1．
  （Ⅰ）證明：PA⊥平面ABCD；
  （Ⅱ）求以AC為棱，EAC與DAC為面的二面角θ的大小；
  （Ⅲ）在棱PC上是否存在一點F，使BF∥平面AEC？證明你的結論．
  組卷：632引用：26難度：0.1

  解析