人教新版九年級上學期《第22章 二次函數》2020年中考真題套卷（2）
發布：2024/11/29 7:30:2
一、選擇題（共10小題）
-
1．如圖所示，拋物線y=ax2+bx+c的頂點為B（-1，3），與x軸的交點A在點（-3，0）和（-2，0）之間，以下結論：
①b2-4ac=0；②a+b+c＞0；③2a-b=0；④c-a=3
其中正確的有（ ）個．組卷：6078引用：39難度：0.9 -
2．用配方法將二次函數y=x2-8x-9化為y=a（x-h）2+k的形式為（ ）
組卷：1705引用：74難度：0.7 -
3．將拋物線y=x2-6x+5向上平移兩個單位長度，再向右平移一個單位長度后，得到的拋物線解析式是（ ）
組卷：3795引用：45難度：0.8 -
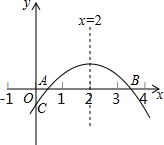4．如圖，二次函數y=ax2+bx+c（a≠0）的圖象與x軸正半軸相交于A、B兩點，與y軸相交于點C，對稱軸為直線x=2，且OA=OC，則下列結論：
①abc＞0；②9a+3b+c＜0；③c＞-1；④關于x的方程ax2+bx+c=0（a≠0）有一個根為-1a
其中正確的結論個數有（ ）組卷：953引用：19難度：0.7 -
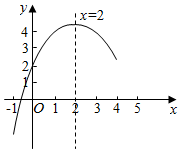5．已知y=ax2+bx+c（a≠0）的圖象如圖所示，對稱軸為直線x=2．若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的兩個根，且x1＜x2，-1＜x1＜0，則下列說法正確的是（ ）組卷：3040引用：27難度：0.6 -
6．設函數y=a（x-h）2+k（a,h,k是實數，a≠0），當x=1時，y=1；當x=8時，y=8，（ ）
組卷：6100引用：35難度：0.6 -
7．已知a,b是非零實數，|a|＞|b|，在同一平面直角坐標系中，二次函數y1=ax2+bx與一次函數y2=ax+b的大致圖象不可能是（ ）
組卷：3446引用：17難度：0.5 -
8．對于題目“一段拋物線L：y=-x（x-3）+c（0≤x≤3）與直線l：y=x+2有唯一公共點，若c為整數，確定所有c的值”，甲的結果是c=1，乙的結果是c=3或4，則（ ）
組卷：4830引用：15難度：0.4 -
9．二次函數y=-（x-1）2+5，當m≤x≤n且mn＜0時，y的最小值為2m,最大值為2n,則m+n的值為（ ）
組卷：8206引用：36難度：0.4 -
10．已知二次函數y=x2，當a≤x≤b時m≤y≤n,則下列說法正確的是（ ）
組卷：5022引用：13難度：0.3
三、解答題（共10小題）
-
29．已知拋物線y=ax2+bx+1經過點（1，-2），（-2，13）．
（1）求a,b的值．
（2）若（5，y1），（m,y2）是拋物線上不同的兩點，且y2=12-y1，求m的值．組卷：4547引用：38難度：0.5 -
30．設a、b是任意兩個實數，用max{a,b}表示a、b兩數中較大者，例如：max{-1，-1}=-1，max{1，2}=2，max{4，3}=4，參照上面的材料，解答下列問題：
（1）max{5，2}=，max{0，3}=；
（2）若max{3x+1，-x+1}=-x+1，求x的取值范圍；
（3）求函數y=x2-2x-4與y=-x+2的圖象的交點坐標，函數y=x2-2x-4的圖象如圖所示，請你在圖中作出函數y=-x+2的圖象，并根據圖象直接寫出max{-x+2，x2-2x-4}的最小值．組卷：3865引用：16難度：0.3