2022-2023學年湖北省襄陽市南漳縣九年級（下）期中數學試卷

一．選擇題（共10小題，滿分30分，每小題3分）

• 1．在Rt△ABC中，∠C=90°，已知AC=2，BC=3，那么下列各式中，正確的是（　　）

  A．sinB= 2 3	B．cosB= 2 3
  C．tanB= 2 3	D．tanB= - 2 13 13
  組卷：563引用：3難度：0.7

  解析

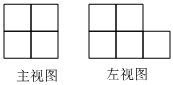• 2．由一些完全相同的小正方體搭成的幾何體，它的主視圖和左視圖如圖所示，組成這個幾何體的小正方體的個數最少和最多分別是（　　）

  A．5，10

  B．6，10

  C．6，9

  D．5，9
  組卷：157引用：3難度：0.6

  解析

• 3．在Rt△ABC中，∠C=90°，AB=2BC，則cosA的值是（　　）

  A． 3 2

  B． 1 2

  C． 2 5 5

  D． 5 5
  組卷：713引用：2難度：0.7

  解析

• 4．小明在星期天上午8：30測得某樹的影長為9m,下午13：00他又測得該樹的影長為4m（如圖所示），若兩次日照的光線互相垂直，則這棵樹的高度為（　　）

  A．8m

  B．6m

  C．4.5m

  D．4m
  組卷：297引用：8難度：0.5

  解析

• 5．在平面直角坐標系中，A（2，n-1）是反比例函數y=

  k

  x

  （k≠0）的圖象上一點，已知點B（2，n），點C（n-1，n），連接BC，則下列說法正確的是（　　）

  A．n的值可能為1

  B．點C不可能在反比例函數 y= k x 的圖象上

  C．在反比例函數 y= k x 的圖象的一個分支上，可能存在y隨x的增大而增大

  D．直線BC與反比例函數y= k x 的圖象必有一個交點
  組卷：93引用：2難度：0.5

  解析

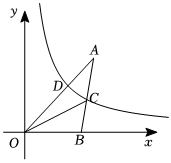• 6．如圖，反比例函數y=

  k

  x

  （k≠0，x＞0）經過△ABO邊AB的中點C，與邊AO交于點D，且OD=2AD，連接OC，若△AOC的面積為

  7

  8

  ，則k=（　　）

  A． 7 4

  B．2

  C． 9 4

  D． 5 2
  組卷：495引用：6難度：0.5

  解析

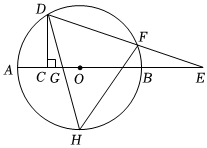• 7．如圖，⊙O直徑AB，DC⊥平分OA，AB延長線上一點E，DE交圓O于F，且EF=OA．弦DH交OC于G，滿足GD²=GO×GE，S_△DHF-S_△DCE=2

  3

  ，AC長為（　　）

  A． 3

  B． 4 3 3

  C．2

  D． 2 3
  組卷：837引用：2難度：0.3

  解析

三．解答題（共8小題，滿分70分）

• 22．問題探究：
  （1）如圖①，點D，E分別是△ABC邊AB，AC上的點，且DE∥BC，

  AD

  =

  1

  3

  BD

  ，則△ADE與△ABC的高之比為

  ；
  （2）如圖②，在△ABC中，BC=10，S_△ABC=50，矩形DEFG的頂點D，E分別在邊AB、AC上，頂點F、G在邊BC上，若設DG=x,求當x取何值時，矩形DEFG面積最大．
  問題解決：
  （3）某市進行綠化改造，美化生態環境．如圖③，現有一塊四邊形的空地ABCD計劃改造公園，經測量AB=50m,BC=100m,CD=72m,且∠B=∠C=60°，按設計要求，要在四邊形公園ABCD內建造一個矩形活動場所PQMN，頂點M、N同在邊BC上，頂點Q、P分別在邊AB、CD上，為了滿足居民需求，計劃在矩形活動場所PQMN中種植草坪，在公園內其它區域種植花卉．已知花卉每平方米200元，草坪每平方米80元，則綠化改造所需費用至少為多少元？（結果保留根號）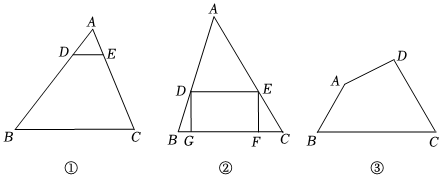
  
  組卷：1057引用：5難度：0.3

  解析

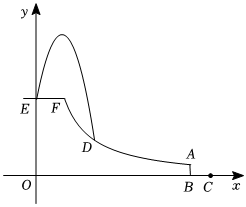• 23．如圖，有一個人站在球臺EF（水平）上去打高爾夫球，球臺到x軸的距離為8米，與y軸相交于點E，彎道FA：

  y

  =

  k

  x

  與球臺交于點F，且EF=3米，彎道末端AB垂直x軸于B，且AB=1.5米，從點E處飛出的紅色高爾夫球沿拋物線L：y=-x²+bx+8運動，落在彎道FA的D處，且D到x軸的距離為4米；
  （1）k的值為

  ；點D的坐標為

  ；b=

  ；
  （2）紅色球落在D處后立即彈起，沿另外一條拋物線G運動，若G的最高點坐標為P（10，5）．
  ①求G的解析式，并說明小球能否落在彎道FA上？
  ②在x軸上有托盤BC=2，若小球恰好能被托盤接住，則把托盤向上平移的距離為d,則d的取值范圍是什么？
  （3）若在紅色球從E處飛出的同時，一黃色球從點E的正上方M（0，m）飛出，它所運行軌跡與拋物線L形狀相同，且黃色球始終在紅色球的正上方，當紅色球到y軸的距離為4米，且黃球位于紅球正上方超過6米的位置時，直接寫出m的取值范圍．
  組卷：393引用：3難度：0.2

  解析