2022-2023學年湖南省長沙市明德教育集團八年級（上）期末數學試卷

一、選擇題（在下列各題的四個選項中，只有一項是正確答案.請在答題卡中填涂符合題意的選項.本大題共10個小題，每小題3分，共30分）

• 1．下列圖形是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：48引用：1難度：0.9

  解析

• 2．以下列長度的三條線段為邊，能組成三角形的是（　　）

  A．1，10，10

  B．2，5，8

  C．1，8，6

  D．2，9，7
  組卷：72引用：1難度：0.6

  解析

• 3．祖沖之發現的圓周率的分數近似值

  355

  113

  ≈3.1415929，稱為密率，比π的值只大0.0000003，0.0000003這個數用科學記數法可表示為（　　）

  A．0.3×10-6

  B．0.3×10-7

  C．3×10-6

  D．3×10-7
  組卷：167引用：5難度：0.9

  解析

• 4．下列運算正確的是（　　）

  A．（x+1）2=x2+1	B．（-2nm2）3=-6n3m6
  C．x?x3=x4	D．a6÷a3=a2
  組卷：389引用：2難度：0.8

  解析

• 5．若分式

  x

  2

  -

  4

  x

  -

  2

  的值為0，則x的值為（　　）

  A．±2

  B．-2

  C．0

  D．2
  組卷：2627引用：25難度：0.9

  解析

• 6．在Rt△ABC中，∠C=90°，∠A=30°，AB=2，則BC=（　　）

  A．1

  B．2

  C． 3

  D． 5
  組卷：422引用：3難度：0.6

  解析

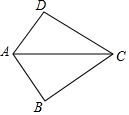• 7．如圖，已知AB=AD，那么添加下列一個條件后，仍無法判定△ABC≌△ADC的是（　　）

  A．CB=CD

  B．∠BAC=∠DAC

  C．∠B=∠D=90°

  D．∠BCA=∠DCA
  組卷：4588引用：129難度：0.7

  解析

• 8．如圖，在△ABC中，BO平分∠ABC，CO平分∠ACB，MN經過點O，與AB、AC相交于點M、N，且MN∥BC．若AB=8，AC=6，BC=10，那么△AMN的周長是（　　）

  A．7

  B．12

  C．14

  D．24
  組卷：507引用：4難度：0.7

  解析

三、解答題（本大題共9個小題，第17、18、19題每小題0分，第20、21題每小題0分，第22、23題每小題0分，第24、25題每小題0分，共72分）

• 24．定義：若兩個等腰三角形的頂角之和等于180°，則稱這兩個等腰三角形互為“友好三角形”，這兩個角的頂點互為“友好點”．
  （1）已知△ABC與△DEF互為“友好三角形”，點B和點E互為“友好點”，且△ABC中有一個內角為50°，則∠DEF=

  °．
  （2）已知，在平面直角坐標系中，點A（0，

  3

  +

  2

  ），B（

  3

  +

  2

  ，0），點P為∠AOB角平分線OM上一動點，點C為x軸上一動點，連接AB，AP，AC．
  ①如圖1，∠APC=90°，求證：△APC與△AOB互為“友好三角形”；
  ②在①的條件下，若點P的坐標為（1，1），求點C的坐標；
  （3）如圖2，在（2）的條件下，將OA繞著點O順時針方向旋轉30°（即∠A'Oy=30°）得到A'O，連接A'P、A'B、PC、A'C，OM為∠A'OB的角平分線，過點P（P點不在點O處）作PE⊥x軸于點E，當點E在線段OB之間（不包含端點），點C在點E左側且A'P=PC時，證明：△A'PC與△A'OB互為“友好三角形”，并說明OA'，OC，EC之間的數量關系．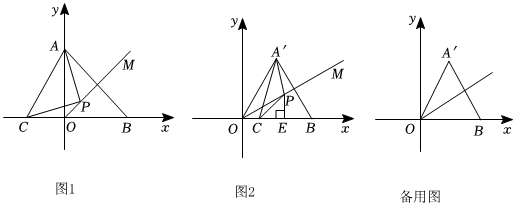
  
  組卷：497引用：1難度：0.2

  解析

• 25．由完全平方公式（a-b）²=a²-2ab+b²可知，a²+b²=（a-b）²+2ab,而（a-b）²≥0，所以，對所有的實數a,b都有：a²+b²≥2ab,且只有當a=b時，才有等號成立：a²+b²=2ab.
  應用上面的結論解答下列問題：
  （1）計算

  （

  x

  -

  1

  x

  ）

  2

  =

  ，由此可知x²+

  1

  x

  2

  2（填不等號）；
  （2）已知m,n為不相等的兩正數，試比較：（1+m%）（1+n%）與

  （

  1

  +

  m

  +

  n

  2

  %

  ）

  （

  1

  +

  m

  +

  n

  2

  %

  ）

  的大小；
  （3）試求分式

  x

  2

  x

  4

  -

  2

  x

  2

  +

  4

  的最大值．
  組卷：666引用：1難度：0.5

  解析