當前位置：試卷中心 > 試卷詳情

2023-2024學年山東省濟南市歷城二中高三（上）開學數學試卷

發布：2024/7/18 8:0:9

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．若集合A={x|x²-3x-10≤0，x∈Z}，B={x|2x²-x-6＞0，x∈Z}，則A∩B的子集有（　　）
A．15個 B．16個 C．7個 D．8個
組卷：93引用：7難度：0.8
解析
2．設復數z的共軛復數為
z
，z（1-i）=3-i,則復數
z
在復平面內的對應點位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：26引用：2難度：0.7
解析
3．若向量
a
、
b
滿足：|
a
|=1，（
a
+
b
）⊥
a
，（2
a
+
b
）⊥
b
，則|
b
|=（　　）
A．2 B．
2
C．1 D．
2
2
組卷：3526引用：47難度：0.7
解析
4．已知A，B，C為△ABC的三個內角，其對邊分別為a,b,c,若
a
2
-
b
2
=
3
bc
，且
sin
（
A
+
B
）
sin
B
=
2
3
，則A=（　　）
A．
π
6
B．
π
3
C．
2
π
3
D．
5
π
6
組卷：80引用：1難度：0.5
解析
5．一對年輕夫婦和其兩歲的孩子做游戲，讓孩子把分別寫有“1”“3”“1”“4”的四張卡片隨機排成一行，若卡片按從左到右的順序排成“1314”，則孩子會得到父母的獎勵，那么孩子受到獎勵的概率為（　　）
A．
1
12
B．
5
12
C．
7
12
D．
5
6
組卷：60引用：4難度：0.8
解析
6．已知函數f（x）=3sinωx在區間[-
π
3
，
π
4
]上的最小值為-3，則ω的取值范圍是（　　）
A．
（
-
∞
，
9
2
]
∪[6，+∞） B．
（
-
∞
，
9
2
]
∪
[
3
2
，
+
∞
）
C．（-∞，-2]∪[6，+∞） D．（-∞，-2]∪
[
3
2
，
+
∞
）
組卷：88引用：2難度：0.5
解析
7．已知函數f（x）是R上的偶函數，且f（x）的圖象關于點（1，0）對稱，當x∈[0，1]時，f（x）=2-2^x，則f（0）+f（1）+f（2）+…+f（2022）的值為（　　）
A．-2 B．-1 C．0 D．1
組卷：431引用：11難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6題，共70分.解答應寫出文字說明、證明過程或演算步驟.

21．已知函數
f
（
x
）
=
sin
（
ωx
-
π
6
）
+
sin
（
ωx
-
π
2
）
滿足
f
（
π
6
）
=
0
，其中0＜ω＜3，將函數y=f（x）的圖象上各點的橫坐標伸長為原來的2倍（縱坐標不變），再將得到的圖象向左平移
π
4
個單位，得到函數y=g（x）的圖象．
（1）求ω；
（2）求函數y=g（x）的解析式；
（3）求g（x）在[
-
π
4
，
3
π
4
]上的最值及相應的x值．
組卷：148引用：2難度：0.5
解析
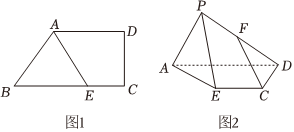22．如圖1，在梯形ABCD中，AD∥BC，∠ABC=60°，AB=AD=2，BC=3，點E在線段BC上，BE=2EC，將△ABE沿AE翻折至△PAE的位置，連接PD，點F為PD中點，連接CF，如圖2．
（1）在線段AD上是否存在一點Q，使平面PAE∥平面FQC？若存在，請確定點Q的位置，若不存在，請說明理由；
（2）當平面PAE⊥平面AECD時，求三棱錐P-AEF的體積．
組卷：90引用：7難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（ - ∞ ， 9 2 ] ∪[6，+∞）	B．（ - ∞ ， 9 2 ] ∪ [ 3 2 ， + ∞ ）
C．（-∞，-2]∪[6，+∞）	D．（-∞，-2]∪ [ 3 2 ， + ∞ ）

2023-2024學年山東省濟南市歷城二中高三（上）開學數學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．若集合A={x|x2-3x-10≤0，x∈Z}，B={x|2x2-x-6＞0，x∈Z}，則A∩B的子集有（ ）

2．設復數z的共軛復數為z，z（1-i）=3-i,則復數z在復平面內的對應點位于（ ）

3．若向量a、b滿足：|a|=1，（a+b）⊥a，（2a+b）⊥b，則|b|=（ ）

4．已知A，B，C為△ABC的三個內角，其對邊分別為a,b,c,若a2-b2=3bc，且sin（A+B）sinB=23，則A=（ ）

5．一對年輕夫婦和其兩歲的孩子做游戲，讓孩子把分別寫有“1”“3”“1”“4”的四張卡片隨機排成一行，若卡片按從左到右的順序排成“1314”，則孩子會得到父母的獎勵，那么孩子受到獎勵的概率為（ ）

6．已知函數f（x）=3sinωx在區間[-π3，π4]上的最小值為-3，則ω的取值范圍是（ ）

7．已知函數f（x）是R上的偶函數，且f（x）的圖象關于點（1，0）對稱，當x∈[0，1]時，f（x）=2-2x，則f（0）+f（1）+f（2）+…+f（2022）的值為（ ）

四、解答題：本題共6題，共70分.解答應寫出文字說明、證明過程或演算步驟.

1．若集合A={x|x²-3x-10≤0，x∈Z}，B={x|2x²-x-6＞0，x∈Z}，則A∩B的子集有（　　）

2．設復數z的共軛復數為
z
，z（1-i）=3-i,則復數
z
在復平面內的對應點位于（　　）

3．若向量
a
、
b
滿足：|
a
|=1，（
a
+
b
）⊥
a
，（2
a
+
b
）⊥
b
，則|
b
|=（　　）

4．已知A，B，C為△ABC的三個內角，其對邊分別為a,b,c,若
a
2
-
b
2
=
3
bc
，且
sin
（
A
+
B
）
sin
B
=
2
3
，則A=（　　）

5．一對年輕夫婦和其兩歲的孩子做游戲，讓孩子把分別寫有“1”“3”“1”“4”的四張卡片隨機排成一行，若卡片按從左到右的順序排成“1314”，則孩子會得到父母的獎勵，那么孩子受到獎勵的概率為（　　）

6．已知函數f（x）=3sinωx在區間[-
π
3
，
π
4
]上的最小值為-3，則ω的取值范圍是（　　）

7．已知函數f（x）是R上的偶函數，且f（x）的圖象關于點（1，0）對稱，當x∈[0，1]時，f（x）=2-2^x，則f（0）+f（1）+f（2）+…+f（2022）的值為（　　）