2023-2024學(xué)年重慶八中高三（上）入學(xué)數(shù)學(xué)試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的。

• 1．若{a²，0，-1}={a,b,0}，則ab的值是（　　）

  A．0

  B．1

  C．-1

  D．±1
  組卷：289引用：3難度：0.8

  解析

• 2．已知f（x）是定義在（0，+∞）上的函數(shù)，g（x）=xf（x），則“f（x）為增函數(shù)”是“g（x）為增函數(shù)”的（　　）

  A．充要條件	B．充分不必要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：217引用：4難度：0.7

  解析

• 3．某大學(xué)有A，B兩個(gè)圖書館，學(xué)生小李周六隨機(jī)選擇一圖書館閱讀，如果周六去A圖書館，那么周日去A圖書館的概率為0.4；如果周六去B圖書館，那么周日去A圖書館的概率為0.6．小李周日去A圖書館的概率為（　　）

  A．0.5

  B．0.24

  C．0.16

  D．0.36
  組卷：264引用：2難度：0.8

  解析

• 4．已知函數(shù)f（x）=log₂（x²-ax+3a）在區(qū)間[2，+∞）上遞增，則實(shí)數(shù)a的取值范圍是（　　）

  A．（-∞，4）

  B．（-4，4）

  C．（-4，4]

  D．[-4，+∞）
  組卷：1380引用：11難度：0.5

  解析

• 5．函數(shù)

  f

  （

  x

  ）

  =

  4

  x

  -

  4

  -

  x

  x

  2

  +

  |

  x

  |

  -

  2

  的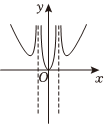圖象大致為（　　）

  A．

  B．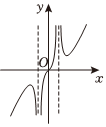

  C．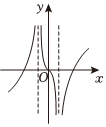

  D．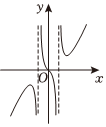
  組卷：29引用：1難度：0.7

  解析

• 6．設(shè)

  a

  =

  ln

  0

  .

  3

  ln

  0

  .

  4

  ，b=0.3^0.4，c=0.4^0.3，則（　　）

  A．a(chǎn)＞c＞b

  B．c＞b＞a

  C．c＞a＞b

  D．a(chǎn)＞b＞c
  組卷：206引用：5難度：0.7

  解析

• 7．2023年1月31日，據(jù)“合肥發(fā)布”公眾號(hào)報(bào)道，我國(guó)最新量子計(jì)算機(jī)“悟空”即將面世，預(yù)計(jì)到2025年量子計(jì)算機(jī)可以操控的超導(dǎo)量子比特達(dá)到1024個(gè)．已知1個(gè)超導(dǎo)量子比特共有2種疊加態(tài)，2個(gè)超導(dǎo)量子比特共有4種疊加態(tài)，3個(gè)超導(dǎo)量子比特共有8種疊加態(tài)，?，每增加1個(gè)超導(dǎo)量子比特，其疊加態(tài)的種數(shù)就增加一倍．若N=a×10^k（1≤a＜10，k∈N），則稱N為k+1位數(shù)，已知1024個(gè)超導(dǎo)量子比特的疊加態(tài)的種數(shù)是一個(gè)m位的數(shù)，則m=（　　）（參考數(shù)據(jù)：lg2≈0.301）

  A．308

  B．309

  C．1023

  D．1024
  組卷：337引用：6難度：0.7

  解析

四、解答題：本題共6小題，共70分。解答應(yīng)寫出文字說明、證明過程或演算步驟。

• 21．已知雙曲線

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的右焦點(diǎn)為F（4，0），P（-3，1）為雙曲線C上一點(diǎn)．
  （1）求C的方程；
  （2）設(shè)直線l：y=kx+m（k≠0），且不過點(diǎn)P，若l與C交于A，B兩點(diǎn)，點(diǎn)B關(guān)于原點(diǎn)的對(duì)稱點(diǎn)為D，若

  PA

  ?

  PD

  =

  0

  ，試判斷k是否為定值，若是，求出k值，若不是，請(qǐng)說明理由．
  組卷：138引用：4難度：0.3

  解析

• 22．已知函數(shù)f（x）=e^x+x,g（x）=ax²+2x+1．
  （1）當(dāng)

  a

  =

  1

  2

  時(shí)，討論函數(shù)F（x）=f（x）-g（x）的單調(diào)性；
  （2）當(dāng)a＜0時(shí)，求曲線y=f（x）與y=g（x）的公切線方程．
  組卷：116引用：2難度：0.4

  解析