2021-2022學年黑龍江省雙鴨山市集賢一中、四中等高二（下）期末數學試卷

一、單選題（每題5分，共40分）

• 1．若

  A

  3

  n

  =

  12

  C

  2

  n

  ，則n等于（　　）

  A．8

  B．4

  C．5或6

  D．3或4
  組卷：380引用：4難度：0.8

  解析

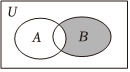• 2．已知全集U=R，集合A={x|x≥2}，B={x|-2＜x＜3}，則圖中陰影部分表示的集合為（　　）

  A．[-2，2]

  B．（-2，2]

  C．（-2，2）

  D．[-2，2）
  組卷：340引用：6難度：0.8

  解析

• 3．第24屆冬奧會奧運村有智能餐廳A，人工餐廳B，運動員甲第一天隨機地選擇一餐廳用餐，如果第一天去A餐廳，那么第二天去A餐廳的概率為0.6；如果第一天去B餐廳，那么第二天去A餐廳的概率為0.5，運動員甲第二天去A餐廳用餐的概率為（　　）

  A．0.75

  B．0.6

  C．0.55

  D．0.45
  組卷：306引用：6難度：0.7

  解析

• 4．在某地舉行的數學競賽中，全體參賽學生的競賽成績近似服從正態分布N（70，100）．已知成績在90分以上（含90分）的學生有14名．參加此次數學競賽的學生數大約為（　　）
  參考數據：P（μ-σ＜X＜μ+σ）≈0.6827；P（μ-2σ＜X＜μ+2σ）≈0.9545；P（μ-3σ＜X＜μ+3σ）≈0.9973

  A．1200

  B．900

  C．600

  D．300
  組卷：30引用：1難度：0.7

  解析

• 5．色差和色度是衡量毛絨玩具質量優劣的重要指標，現抽檢一批產品測得數據列于表中：已知該產品的色度y和色差x之間滿足線性相關關系，且

  ?

  y

  =

  0

  .

  8

  x

  +

  ?

  a

  ，現有一對測量數據為（30，23.6），則該數據的殘差為（　　）
  

  色差x	21	23	25	27
  色度y	15	18	19	20

  A．-0.96

  B．-0.8

  C．0.8

  D．0.96
  組卷：145引用：8難度：0.8

  解析

• 6．已知實數a,b滿足1≤a+b≤3，-1≤a-b≤1，則4a+2b的取值范圍是（　　）

  A．[0，10]

  B．[2，10]

  C．[0，12]

  D．[2，12]
  組卷：265引用：6難度：0.8

  解析

• 7．已知關于x的不等式ax²+bx+c＞0的解集為（-2，4），則不等式cx²-bx+a＜0的解集是（　　）

  A．{x|x＜- 1 2 或x＞ 1 4 }	B．{ x|- 1 4 ＜x＜ 1 2 }
  C．{x|x＜- 1 4 或x＞ 1 2 }	D．{x|- 1 2 ＜x＜ 1 4 }
  組卷：938引用：5難度：0.7

  解析

四、解答題（共70分）

• 21．2022年北京冬奧組委發布的《北京2022年冬奧會和冬殘奧會經濟遺產報告（2022）》顯示，北京冬奧會簽約了50家贊助企業，為了解這50家贊助企業每天的銷售額與每天線上銷售時間之間的相關關系，某平臺對這50家贊助企業進行跟蹤調查，其中每天線上銷售時間不少于8小時的企業有20家，剩下的企業中，每天的銷售額不足30萬元的企業占這剩下的企業數量的

  3

  5

  ，統計后得到如下2×2列聯表．

  每天線上銷售時間	每天銷售額		合計
  	不少于30萬元	不足30萬元
  不少于8小時	18
  不足8小時
  合計

  （1）完成列聯表，并依據小概率值α=0.001的獨立性檢驗，能否認為贊助企業每天的銷售額與每天線上銷售時間有關？
  （2）按每天線上銷售時間進行分層抽樣，在上述贊助企業中抽取5家企業，再從這5家企業中抽取2家企業，求抽取的2家企業中至少有1家企業每天線上銷售時間不少于8小時的概率．
  參考公式及數據：χ²=

  n

  （

  ad

  -

  bc

  ）

  2

  （

  a

  +

  b

  ）

  （

  c

  +

  d

  ）

  （

  a

  +

  c

  ）

  （

  b

  +

  d

  ）

  ，其中n=a+b+c+d.
  

  a	0.1	0.05	0.01	0.005	0.001
  x0	2.706	3.841	6.635	7.879	10.828
  組卷：54引用：5難度：0.8

  解析

• 22．應對嚴重威脅人類生存與發展的氣候變化，其關鍵在于“控碳”，其必由之路是先實現“碳達峰”，而后實現“碳中和”，2020年第七十五屆聯合國大會上，我國向世界鄭重承諾：力爭在2030年前實現“碳達峰”，努力爭取在2060年前實現“碳中和”，近年來，國家積極發展新能源汽車，某品牌的新能源汽車某區域銷售在2021年11月至2022年3月這5個月的銷售量y（單位：百輛）的數據如下表：
  

  月份	2021年11月	2021年12月	2022年1月	2022年2月	2022年3月
  月份代碼：x	1	2	3	4	5
  銷售量y（單位：百輛）	45	56	64	68	72

  （1）依據表中的統計數據，請判斷月份代碼x與該品牌的新能源汽車區域銷售量y（單位；百輛）是否具有較高的線性相關程度？
  （參考：若0.30＜|r|＜0.75，則線性相關程度一般，若|r|≥0.75，則線性相關程度較高，計算r時精確度為0.01．）
  （2）求銷售量y與月份代碼x之間的線性回歸方程，并預測2022年4月份該區域的銷售量（單位：百輛）．
  參考數據：

  5

  ∑

  i

  =

  1

  （y_i-

  y

  ）²=460，

  5

  ∑

  i

  =

  1

  （x_i-

  x

  ）（y_i-

  y

  ）=66，

  46

  ≈

  6

  .

  78

  ，
  參考公式：相關系數r=

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  （

  y

  i

  -

  y

  ）

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  n

  ∑

  i

  =

  1

  （

  y

  i

  -

  y

  ）

  2

  ，
  線性回歸方程

  ?

  y

  =

  ?

  b

  x

  +

  ?

  a

  中，

  ∧

  b

  =

  n

  ∑

  i

  =

  1

  x

  i

  y

  i

  -

  n

  x

  y

  n

  ∑

  i

  =

  1

  x

  i

  2

  -

  n

  x

  2

  =

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  （

  y

  i

  -

  y

  ）

  n

  ∑

  i

  =

  1

  （

  x

  i

  -

  x

  ）

  2

  ，

  ∧

  a

  =

  y

  -

  ∧

  b

  x

  ，其中

  x

  ，

  y

  為樣本平均值．
  組卷：47引用：5難度：0.5

  解析