2012-2013學(xué)年山東省煙臺(tái)市牟平區(qū)高三（上）模塊檢測(cè)數(shù)學(xué)試卷（理科）

一、選擇題：本大題共12小題；每小題5分，共60分，在每小題給出的個(gè)選項(xiàng)中，只有一個(gè)選項(xiàng)符合題目要求，把正確選項(xiàng)的代號(hào)涂在答題卡上．

• 1．已知函數(shù)f（x）=lg（1-x）的定義域?yàn)镸，函數(shù)

  y

  =

  1

  x

  的定義域?yàn)镹，則M∩N=（　　）

  A．{x|x＜1且x≠0}

  B．{x|x≤1且x≠0}

  C．{x|x＞1}

  D．{x|x≤1}
  組卷：1215引用：15難度：0.9

  解析

• 2．設(shè)a=2^2.5，b=2.5⁰，c=

  （

  1

  2

  ）

  2

  .

  5

  ，則a,b,c的大小關(guān)系是（　　）

  A．a(chǎn)＞c＞b

  B．c＞a＞b

  C．a(chǎn)＞b＞c

  D．b＞a＞c
  組卷：242引用：25難度：0.9

  解析

• 3．曲線

  y

  =

  （

  1

  2

  ）

  x

  在x=0點(diǎn)處的切線方程是（　　）

  A．x+yln2-ln2=0	B．xln2+y-1=0
  C．x-y+1=0	D．x+y-1=0
  組卷：18引用：11難度：0.9

  解析

• 4．已知向量

  a

  、

  b

  ，其中|

  a

  |=

  2

  ，|

  b

  |=2，且（

  a

  -

  b

  ）⊥

  a

  ，則向量

  a

  和

  b

  的夾角是（　　）

  A． π 4

  B． π 6

  C． 3 π 4

  D． 5 π 6
  組卷：327引用：35難度：0.7

  解析

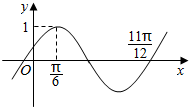• 5．函數(shù)f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜

  π

  2

  ）的部分圖象如圖示，則將y=f（x）的圖象向右平移

  π

  6

  個(gè)單位后，得到的圖象解析式為（　　）

  A．y=sin2x	B．y=cos2x
  C．y=sin（2x+ 2 π 3 ）	D．y=sin（2x- π 6 ）
  組卷：404引用：70難度：0.9

  解析

• 6．已知向量

  a

  =

  （

  x

  -

  1

  ，

  2

  ）

  ，

  b

  =

  （

  4

  ，

  y

  ）

  ，

  若

  a

  ⊥

  b

  ，

  則

  9

  x

  +

  3

  y

  的最小值為（　　）

  A． 2 3

  B．6

  C．12

  D． 3 2
  組卷：50引用：22難度：0.9

  解析

• 7．已知sin2α=-

  24

  25

  ，α∈（-

  π

  4

  ，0），則sinα+cosα=（　　）

  A． 1 5

  B．- 1 5

  C．- 7 5

  D． 7 5
  組卷：576引用：37難度：0.9

  解析

三、解答題：本大題共6小題，共74分．解答時(shí)要求寫出必要的文字說明，證明過程或推理步驟．

• 21．已知函數(shù)g（x）=ax²-2ax+1+b（a＞0）在區(qū)間[2，3]上的最大值為4，最小值為1，記f（x）=g（|x|）
  （Ⅰ）求實(shí)數(shù)a,b的值；
  （Ⅱ）若不等式f（log₂k）＞f（2）成立，求實(shí)數(shù)k的取值范圍；
  （Ⅲ）定義在[p,q]上的一個(gè)函數(shù)m（x），用分法T：p=x₀＜x₁＜…＜x_i＜…＜x_n=q將區(qū)間[p,q]任意劃分成n個(gè)小區(qū)間，如果存在一個(gè)常數(shù)M＞0，使得和式

  n

  ∑

  i

  =

  1

  |

  m

  （

  x

  i

  ）

  -

  m

  （

  x

  i

  -

  1

  ）

  |

  ≤

  M

  恒成立，則稱函數(shù)m（x）為在[p,q]上的有界變差函數(shù)，試判斷函數(shù)f（x）是否為在[1，3]上的有界變差函數(shù)？若是，求M的最小值；若不是，請(qǐng)說明理由．（參考公式：

  n

  ∑

  i

  =

  1

  f

  （

  x

  ）

  =

  f

  （

  x

  1

  ）

  +

  f

  （

  x

  2

  ）

  +

  …+f（x_n））
  組卷：142引用：14難度：0.1

  解析

• 22．已知函數(shù)f（x）=

  lnx

  +

  a

  x

  （a∈R）．
  （1）求f（x）的極值；
  （2）若函數(shù)f（x）的圖象與函數(shù)g（x）=1的圖象在區(qū)間（0，e²]上有公共點(diǎn)，求實(shí)數(shù)a的取值范圍．
  組卷：112引用：13難度：0.1

  解析