2022-2023學年重慶一中高一（下）第一次月考數學試卷（3月份）

一、單項選擇題：本題共8小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合題目要求的.

• 1．已知a∈R，（1+ai）i=3+i（i為虛數單位），則a=（　　）

  A．-1

  B．1

  C．-3

  D．3
  組卷：2610引用：19難度：0.9

  解析

• 2．已知矩形ABCD中，

  AE

  =

  EB

  ，線段AC和DE交于點F，則

  BF

  =（　　）

  A． - 1 3 AB + 2 3 AD

  B． 1 3 AB - 2 3 AD

  C． 2 3 AB - 1 3 AD

  D． - 2 3 AB + 1 3 AD
  組卷：174引用：1難度：0.7

  解析

• 3．若向量

  a

  ，

  b

  滿足|

  a

  |=

  2

  ，|

  b

  |=2，

  a

  ⊥（

  a

  -

  b

  ），則

  a

  與

  b

  的夾角為（　　）

  A． π 4

  B． π 3

  C． 2 π 3

  D． 3 π 4
  組卷：288引用：4難度：0.8

  解析

• 4．將函數

  f

  （

  x

  ）

  =

  3

  sin

  2

  x

  -

  2

  co

  s

  2

  x

  圖象上各點的橫坐標伸長到原來的3倍（縱坐標不變），再向右平移

  π

  8

  個單位長度，則所得函數圖象的一個對稱中心為（　　）

  A． （ 3 π 8 ， 0 ）

  B．（- 3 π 8 ，-1）

  C． （ - 3 π 8 ， 0 ）

  D．（ 3 π 8 ，-1）
  組卷：237引用：5難度：0.8

  解析

• 5．已知

  a

  =

  （

  sinα

  ，

  1

  -

  4

  cos

  2

  α

  ）

  ，

  b

  =

  （

  1

  ，

  3

  sinα

  -

  2

  ）

  ，

  α

  ∈

  （

  0

  ，

  π

  2

  ）

  ，若

  a

  ∥

  b

  ，則

  sin

  2

  α

  2

  +

  cos

  2

  α

  =（　　）

  A． 2 11

  B． 4 11

  C． 6 11

  D． 8 11
  組卷：199引用：6難度：0.7

  解析

• 6．設A₁、A₂、A₃、A₄為平面直角坐標系中兩兩不同的點，若

  A

  1

  A

  3

  =

  λ

  A

  1

  A

  2

  （

  λ

  ∈

  R

  ）

  ，

  A

  1

  A

  4

  =

  μ

  A

  1

  A

  2

  （

  μ

  ∈

  R

  ）

  ，且

  1

  λ

  +

  1

  μ

  =

  4

  ，則稱點A₃、A₄和諧分割點A₁、A₂.已知平面上兩兩不同的點A、B、C、D，若C、D和諧分割點A、B．則下面說法正確的是（　　）

  A．點C可能是線段AB的中點

  B．點C可能是靠近點A的線段AB的三等分點

  C．點C、D可能同時在線段AB上

  D．點C、D可能同時在線段AB的延長線上
  組卷：127引用：3難度：0.5

  解析

• 7．在△ABC中，角A，B，C的對邊分別為a,b,c,已知（sinA+sinB）（a-b）=sinC（b+c），若角A的內角平分線AD的長為3，則b+c的最小值為（　　）

  A．12

  B．24

  C．27

  D．36
  組卷：502引用：6難度：0.5

  解析

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

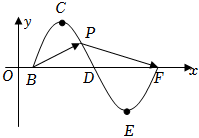• 21．已知函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的圖象如圖所示，點B，D，F為f（x）與x軸的交點，點C，E分別為f（x）的最高點和最低點，而函數f（x）的相鄰兩條對稱軸之間的距離為2，且其在

  x

  =

  -

  1

  2

  處取得最小值．
  （1）求參數ω和φ的值；
  （2）若A=1，求向量

  2

  BC

  -

  CD

  與向量

  BC

  +

  3

  CD

  夾角的余弦值；
  （3）若點P為函數f（x）圖象上的動點，當點P在C，E之間運動時，

  BP

  ?

  PF

  ≥1恒成立，求A的取值范圍．
  組卷：426引用：11難度：0.3

  解析

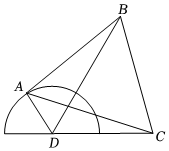• 22．為提升城市旅游景觀面貌，城建部門擬對一公園進行改造，已知原公園是直徑為200米的半圓，出入口在圓心D處，C點為一居民小區，CD距離為200米，按照設計要求，取圓弧上一點A，并以線段AC為一邊向圓外作等邊三角形ABC，使改造之后的公園成四邊形ABCD，并將△BCD區域建成免費開放的植物園，如圖所示．
  （1）若DA⊥DC時，點B與出入口D的距離為多少米？
  （2）A設計在什么位置時，免費開放的植物園區域△BCD面積最大？并求此最大面積．
  組卷：106引用：3難度：0.4

  解析