新人教版九年級上冊《第22章 二次函數(shù)》2019年單元測試卷（四川省綿陽外國語學(xué)校）

一．選擇題

• 1．若關(guān)于x的函數(shù)y=（2-a）x²-x是二次函數(shù)，則a的取值范圍是（　　）

  A．a(chǎn)≠0

  B．a(chǎn)≠2

  C．a(chǎn)＜2

  D．a(chǎn)＞2
  組卷：6329引用：28難度：0.9

  解析

• 2．拋物線y=-3x²-4的開口方向和頂點坐標(biāo)分別是（　　）

  A．向下，（0，-4）	B．向下，（0，4）
  C．向上，（0，4）	D．向上，（0，-4）
  組卷：2643引用：4難度：0.8

  解析

• 3．要由拋物線y=2x²得到拋物線y=2（x+1）²-3，則拋物線y=2x²必須（　　）

  A．向左平移1個單位，再向下平移3個單位

  B．向右平移1個單位，再向上平移3個單位

  C．向右平移1個單位，再向下平移3個單位

  D．向左平移1個單位，再向上平移3個單位
  組卷：1271引用：2難度：0.7

  解析

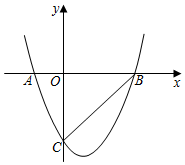• 4．如圖，二次函數(shù)y=x²-2x-3的圖象與x軸交于A、B兩點，與y軸交于點C，則下列說法錯誤的是（　　）

  A．AB=4

  B．∠OCB=45°

  C．當(dāng) x＞3 時，y＞0

  D．當(dāng) x＞0 時，y 隨 x 的增大而減小
  組卷：1016引用：5難度：0.7

  解析

• 5．已知二次函數(shù)y=-（x-k+2）（x+k）+m,其中k,m為常數(shù)．下列說法正確的是（　　）

  A．若k≠1，m≠0，則二次函數(shù)y的最大值小于0

  B．若k＜1，m＞0，則二次函數(shù)y的最大值大于0

  C．若k=1，m≠0，則二次函數(shù)y的最大值小于0

  D．若k＞1，m＜0，則二次函數(shù)y的最大值大于0
  組卷：2249引用：7難度：0.7

  解析

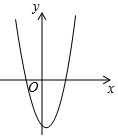• 6．已知函數(shù)y=（x-a）（x-b）（其中a＞b）的圖象如圖所示，則函數(shù)y=ax+b的圖象大致是（　　）

  A．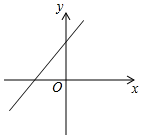

  B．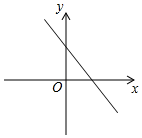

  C．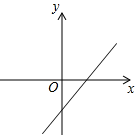

  D．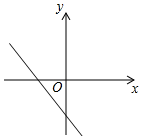
  組卷：1830引用：5難度：0.6

  解析

• 7．已知二次函數(shù)的圖象如圖所示，那么此函數(shù)的解析式只可能是（　　）

  A．y=-x2+x+3

  B．y=-x2-x-3

  C．y=-x2-x+3

  D．y=x2+x+3
  組卷：1110引用：3難度：0.6

  解析

• 8．二次函數(shù)y=x²-2x的頂點坐標(biāo)是（　　）

  A．（1，1）

  B．（1，-1）

  C．（-1，-1）

  D．（-1，1）
  組卷：2514引用：7難度：0.6

  解析

三．解答題

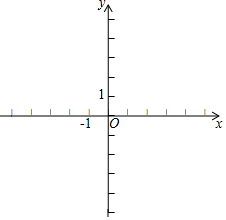• 25．已知拋物線y₁=x²-（m+3）x+3m（m＜0）與直線y₂=kx-3k均經(jīng)過某個定點B．
  （1）求定點B的坐標(biāo)；
  （2）設(shè)y₁與y₂的另一個交點為A，當(dāng)k-m=2時，線段AB（含端點A，B）上至少存在4個橫坐標(biāo)為整數(shù)的點，求m的最大值；
  （3）在（2）的條件下，將線段AB在AB所在的直線上移動，得到線段AB′（A的對應(yīng)點為A′，B的對應(yīng)點為B′），使線段A′B′與拋物線y₁的對稱軸始終有交點，求點B′到直線OA′的距離h的取值范圍．
  組卷：252引用：2難度：0.6

  解析

• 26．已知二次函數(shù)y=ax²+bx-3（a≠0）中x,y滿足下表：
  

  x	…	-4	-3	-2	-1	0	1	2	3	…
  y	…	5	0	-3	-4	-3	0	m	12	…

  （1）請求出m的值；
  （2）某同學(xué)根據(jù)上表數(shù)據(jù)，在如圖所示的平面直角坐標(biāo)系中描點，并畫出了該二次函數(shù)圖象的一部分，請觀察圖象直接寫出當(dāng)y＞0時，x的取值范圍；
  （3）求出這個二次函數(shù)的解析式（也稱為函數(shù)關(guān)系式）．
  組卷：206引用：2難度：0.5

  解析