2022-2023學年浙江省溫州十二中三校聯盟八年級（下）期中數學試卷

一、選擇題（本題有10小題，每小題3分，共30分，每小題只有一個選項是正確的，不選、多選、錯選，均不給分）

• 1．在下列方程中，屬于一元二次方程的是（　　）

  A． 2 x 2 + x = 1 x - 5	B．x2-3x+2
  C．-5x2+3y-2=0	D．y2=16
  組卷：196引用：3難度：0.6

  解析

• 2．若二次根式

  x

  -

  3

  有意義，則實數x的取值范圍是（　　）

  A．x≠3

  B．x＞3

  C．x≥3

  D．x＜3
  組卷：73引用：6難度：0.7

  解析

• 3．

  （

  -

  4

  ）

  2

  的化簡結果是（　　）

  A．4

  B．-4

  C．16

  D．-16
  組卷：453引用：5難度：0.8

  解析

• 4．一組數據2，2，2，3，4，8，12，若加入一個整數n,一定不會發生變化的統計量是（　　）

  A．眾數

  B．平均數

  C．中位數

  D．方差
  組卷：121引用：5難度：0.7

  解析

• 5．下列方程中，有兩個不相等的實數根的是（　　）

  A．x2+5=1

  B．x2+2x-5=0

  C．（x-6）2=0

  D．x2+2x+3=0
  組卷：81引用：2難度：0.6

  解析

• 6．比較2

  2

  ，3，

  7

  的大小，正確的是（　　）

  A． 7 ＜3＜2 2

  B．2 2 ＜ 7 ＜3

  C． 7 ＜2 2 ＜3

  D．2 2 ＜3＜ 7
  組卷：761引用：14難度：0.9

  解析

• 7．關于x的一元二次方程x²+x+a²-18=0的一個根是1，則a的值是（　　）

  A．4

  B．2或-2

  C．4或-4

  D． 3 2
  組卷：281引用：3難度：0.8

  解析

• 8．用配方法解一元二次方程x²-8x+9=0，變形后的結果正確的是（　　）

  A．（x-4）2=-7

  B．（x-4）2=25

  C．（x+4）2=7

  D．（x-4）2=7
  組卷：1034引用：14難度：0.6

  解析

ж三：解答題（本題有6小題，共46分，解答需寫出必要的文字說明、演算步驟或證明過程）

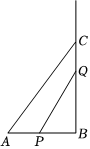• 23．如圖，在△ABC中，∠B=90°，AB=6 cm,BC=8 cm.點P從點A開始沿AB邊向點B以1 cm/s的速度移動，與此同時，點Q從點B開始沿射線BC以2 cm/s的速度移動．當點P停止移動時，點Q同時停止．點P，Q分別從A，B同時出發，經過時間為t秒．
  （1）用t表示△PBQ的面積；
  （2）當t為何值時，以點A，P，Q，C為頂點的四邊形面積為19 cm²；
  （3）在移動過程中線段PQ長度的最小值為

  cm.
  組卷：178引用：2難度：0.1

  解析

• 24．根據以下材料，完成題目．
  材料一：數學家拉為了解決一元二次方程x²=-1在實數范圍內無解的問題，引進虛數單位i,規定i²=-1．當b≠0時，形如a+bi（a,b為實數）的數統稱為虛數．比如5i,3+2i,

  1

  -

  2

  i

  ．當b=0時，a+bi=a+0?i=a為實數．
  材料二：虛數的運算與整式的運算類似，任意兩個虛數a+bi,c+di（其中a,b,c,d為實數．且b≠0，d≠0）有如下運算法則：
  （a+bi）+（c+di）=（a+c）+（b+d）i；
  （a+bi）-（c+di）=（a-c）+（b-d）i；
  （a+bi）?（c+di）=ac+adi+bci+bdi²=（ac-bd）+（ad+bc）i；
  材料三：關于x的一元二次方程ax²+bx+c=0（a,b,c為實數）如果沒有實數根，那么它有兩個虛數根，求根公式為

  x

  =

  -

  b

  ±

  4

  ac

  -

  b

  2

  ?

  i

  2

  a

  ．
  解答以下問題：
  （1）填空：化簡i⁴=

  ，（1+i）²=

  ；
  （2）關于x的一元二次方程x²+mx+n=0有一個根是1+i,其中m,n是實數，求m+n的值；
  （3）已知關于x的一元二次方程x²-3x-k+4=0無實數根，且k為正整數，求該方程的虛數根．
  組卷：594引用：4難度：0.6

  解析