當前位置：試卷中心 > 試卷詳情

2023-2024學年北京市順義一中高一（上）期中數學試卷

發布：2024/10/4 16:0:1

一、選擇題（每小題4分，共40分，四個選項中，只有一項是符合題目要求的）

1．設集合A≡{x|x＜3x-1}，B={x|-1＜x＜3}，則A∩B=（　　）
A．（-1，+∞） B．
（
1
2
，
3
）
C．（-∞，3） D．
（
-
1
，
1
2
）
組卷：30引用：1難度：0.8
解析
2．下列函數是偶函數且在（0，+∞）單調遞減的是（　　）
A．y=x² B．y=x C．
y
=
1
x
D．y=-x²+1
組卷：11引用：1難度：0.7
解析
3．若f（x）與g（x）是同一個函數，且f（x）=x,則g（x）可以是（　　）
A．
g
（
x
）
=
（
x
）
2
B．
g
（
x
）
=
3
x
3
C．
g
（
x
）
=
x
2
D．
g
（
x
）
=
x
2
x
組卷：85引用：3難度：0.9
解析
4．電訊資費調整后，市內通話費的收費標準為：通話時間不超過3分鐘收費0.2元；超過3分鐘以后，每增加1分鐘收費0.1元，不足1分鐘按1分鐘計費．按此標準，通話收費S（元）與通話時間t（分鐘）的函數的大致圖象可表示為（　　）
A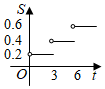． B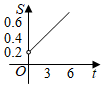． C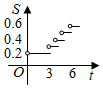． D．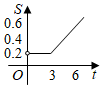
組卷：164引用：5難度：0.9
解析
5．已知冪函數f（x）=x^a圖像經過點（3，
1
9
），則下列命題正確的有（　　）
A．函數f（x）為增函數
B．函數f（x）為偶函數
C．若x＞1，則f（x）＞1
D．若0＜x₁＜x₂，則
f
（
x
1
）
+
f
（
x
2
）
2
＞f（
x
1
+
x
2
2
）
組卷：247引用：4難度：0.7
解析
6．已知p：x≥k,q：
2
-
x
x
+
1
＜0，如果p是q的充分不必要條件，則k的取值范圍是（　　）
A．[2，∞） B．（2，+∞） C．[1，+∞） D．（-∞，-1]
組卷：159引用：3難度：0.8
解析
7．奇函數f（x）在（0，+∞）上單調遞增，且f（1）=0，則不等式
f
（
x
）
-
f
（
-
x
）
x
＞0的解集為（　　）
A．（-1，0）∪（1，+∞） B．（-∞，-1）∪（0，1）
C．（-1，0）∪（0，1） D．（-∞，-1）∪（1，+∞）
組卷：17引用：4難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（共6小題，共85分，解答應寫出文字說明，演算步驟或證明過程）

20．2021年3月1日，國務院新聞辦公室舉行新聞發布會，工業和信息化部提出了芯片發展的五項措施，進一步激勵國內科技巨頭加大了科技研發投入的力度．根據市場調查某數碼產品公司生產某款運動手環的年固定成本為50萬元，每生產1萬只還需另投入20萬元．若該公司一年內共生產該款運動手環x萬只并能全部銷售完，平均每萬只的銷售收入為R（x）萬元，且
R
（
x
）
=
100
-
kx
,
0
＜
x
≤
20
2100
x
-
9000
k
x
2
，
x
＞
20
．當該公司一年內共生產該款運動手環5萬只并全部銷售完時，年利潤為300萬元．
（1）求出k的值并寫出年利潤W（萬元）關于年產量x（萬部）的函數解析式W（x）；
（2）當年產量為多少萬只時，公司在該款運動手環的生產中所獲得的利潤最大？并求出最大利潤．
組卷：282引用：14難度：0.6
解析
21．對于正整數集合A，記A-{a}={x|x∈A，x≠a}，記集合X所有元素之和為S（X），S（?）=0．若?x∈A，存在非空集合A₁、A₂，滿足：①A₁∩A₂=?；②A₁∪A₂=A-{x}；③S（A₁）=S（A₂）稱A存在“雙拆”．若?x∈A，A均存在“雙拆”，稱A可以“任意雙拆”．
（1）判斷集合{1，2，3，4}和{1，3，5，7，9，11}是否存在“雙拆”？如果是，繼續判斷可否“任意雙拆”？（不必寫過程，直接寫出判斷結果）；
（2）A={a₁，a₂，a₃，a₄，a₅}，證明：A不能“任意雙拆”；
（3）若A可以“任意雙拆”，求A中元素個數的最小值．
組卷：263引用：5難度：0.3
解析