2022年吉林省長春市高考數學質檢試卷（理科）（五）

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知集合A={0，1，2}，B={x|-3＜x＜2}，則A∩B子集的個數為（　　）

  A．3

  B．4

  C．7

  D．8
  組卷：81引用：2難度：0.9

  解析

• 2．若z=1+i,則|z²-2z+1|=（　　）

  A．0

  B．1

  C． 2

  D．2
  組卷：78引用：3難度：0.8

  解析

• 3．已知sin（θ-

  π

  2

  ）=

  1

  3

  ，θ∈（0，π），則tanθ=（　　）

  A．2 2

  B． 2 4

  C．-2 2

  D．- 2 4
  組卷：333引用：2難度：0.7

  解析

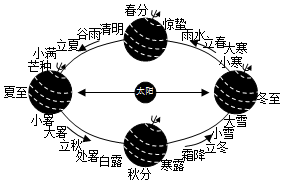• 4．2022年北京冬奧會開幕式倒計時環節把二十四節氣與古詩詞、古諺語融為一體，巧妙地呼應了今年是第二十四屆冬奧會，更是把中國傳統文化和現代美學完美地結合起來，彰顯了中華五千年的文化自信．地球繞太陽的軌道稱為黃道，而二十四節氣正是按照太陽在黃道上的位置來劃分的．當太陽垂直照射赤道時定為“黃經零度”，即春分點．從這里出發，每前進15度就為一個節氣，從春分往下依次順延，清明、谷雨、立夏等等．待運行一周后就又回到春分點，此為一回歸年，共360度，因此分為24個節氣，則今年高考前一天芒種為黃經（　　）

  A．60度

  B．75度

  C．270度

  D．285度
  組卷：25引用：2難度：0.8

  解析

• 5．當圓x²+y²=4截直線l：x-my+m-1=0（m∈R）所得的弦長最短時，m的值為（　　）

  A． - 2

  B． 2

  C．-1

  D．1
  組卷：293引用：2難度：0.7

  解析

• 6．已知等差數列{a_n}的前n項和為S_n，且a₁=d=9，若S_3n-S_2n=S_2n-S_n+729，則n的值為（　　）

  A．8

  B．9

  C．16

  D．18
  組卷：110引用：2難度：0.6

  解析

• 7．甲、乙兩名籃球運動員在8場比賽中的得分用莖葉圖表示，莖葉圖中甲的得分有部分數據丟失，但甲得分的折線圖完好，則下列結論正確的是（　　）
  

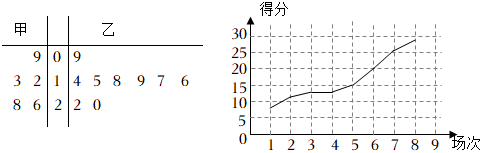
  A．甲得分的極差是11

  B．甲的單場平均得分比乙低

  C．甲有3場比賽的單場得分超過20

  D．乙得分的中位數是16.5
  組卷：111引用：6難度：0.8

  解析

（二）選考題：共10分，請考生在22、23題中任選一題作答，如果多做則按所做的第一題計分．[選修4-4：坐標系與參數方程]

• 22．已知曲線C₁：

  x

  2

  4

  +

  y

  2

  9

  =1（x＞0）經過變換

  x ′ = 1 2 x

  y ′ = 1 3 y

  得到曲線C₂，曲線C₃的參數方程為

  x = t + 1 t

  y = t - 1 t

  （t＞0）．
  （1）寫出曲線C₂的極坐標方程，曲線C₃的普通方程；
  （2）已知直線

  y

  =

  3

  3

  x

  分別與曲線C₂、C₃交于A、B兩點，直線y=-

  3

  3

  x分別與曲線C₂、C₃交于C、D兩點，求四邊形ABCD的面積．
  組卷：147引用：2難度：0.6

  解析

[選修4-5：不等式選講]（10分）

• 23．已知函數f（x）=|x+1|+|2x-3|，M為不等式f（x）≤4的解集．
  （1）求M；
  （2）若a,b∈R，且a²+b²∈M，證明：0≤a²-ab+b²≤3．
  組卷：28引用：5難度：0.5

  解析