2022-2023學年四川省成都市樹德中學高一(下)段考數學試卷(5月份)
發布:2024/7/7 8:0:9
一、單選題:本題共8小題,每小題5分,共40分.在每個小題給出的四個選項中,只有一項是符合題目要求的.
-
1.已知第二象限角α的終邊與單位圓交于
,則sin2α=( )P(m,35)A. -1225B. -2425C. 1225D. 2425組卷:106引用:5難度:0.7 -
2.已知復數
(i是虛數單位)的共軛復數是z=i3-i,則z的虛部是( )z-zA. 35iB. 35C. 25D. -25組卷:60引用:3難度:0.7 -
3.已知向量
,a滿足b,|a|=2,|b|=3,則a?b=1在b上的投影向量為( )aA. -14aB. -19aC. 14aD. 19a組卷:95引用:6難度:0.7 -
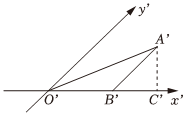 4.如圖是利用斜二測畫法畫出的△ABO的直觀圖,已知A'B'∥y'軸,O'B'=4,且△ABO的面積為16,過A'作A'C'⊥O'B',垂足為點C',則A'C'的長為( )
4.如圖是利用斜二測畫法畫出的△ABO的直觀圖,已知A'B'∥y'軸,O'B'=4,且△ABO的面積為16,過A'作A'C'⊥O'B',垂足為點C',則A'C'的長為( )A. 22B. 2C. 162D.1 組卷:176引用:5難度:0.8 -
5.瑞士數學家歐拉發現的歐拉公式:eiθ=cosθ+isinθ(θ∈R),其中i為虛數單位,e是自然對數的底數.公式非常巧妙地將三角函數與復指數函數關聯了起來,被譽為“數學中的天橋”.下列說法正確的是( )
A.eix+1=0 B. (12+32i)3=1C. 的模長為eiπ3+i12D. sinx=eix+e-ix2組卷:9引用:2難度:0.8 -
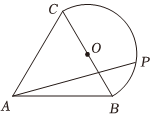 6.如圖所示,邊長為2的正△ABC,以BC的中點O為圓心,BC為直徑在點A的另一側作半圓弧,點P在圓弧上運動,則?BC?AB的取值范圍為( )AP
6.如圖所示,邊長為2的正△ABC,以BC的中點O為圓心,BC為直徑在點A的另一側作半圓弧,點P在圓弧上運動,則?BC?AB的取值范圍為( )APA. [2,23]B.[2,4] C.[2,5] D. [4,33]組卷:772引用:6難度:0.5 -
7.在△ABC中,內角A,B,C的對邊分別為a,b,c,若
,3sinB+2cos2B2=3,則△ABC的外接圓的面積為( )cosBb+cosCc=sinAsinB6sinCA.12π B.16π C.24π D.64π 組卷:624引用:10難度:0.5
四、解答題:本題共6小題,第17小題10分,其余小題每題12分,共70分.解答題應寫出文字說明、證明過程或演算步驟.
-
21.已知函數
的相鄰兩對稱軸間的距離為f(x)=3sin(ωx+π3)+2sin2(ωx2+π6)-1,ω>0.π2
(1)求f(x)的解析式和單調遞增區間;
(2)將函數f(x)的圖像向右平移個單位長度,再把各點的橫坐標縮小為原來的π6(縱坐標不變),得到函數y=g(x)的圖像,若方程12在g(x)=43上的根從小到大依次為,x1,x2,…,xn,若m=x1+2x2+2x3+…+2xn-1+xn,試求n與m的值.x∈[π6,4π3]組卷:27引用:2難度:0.4 -
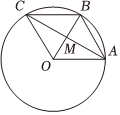 22.如圖,A,B是單位圓上的相異兩定點(O為圓心),∠AOB=θ(),點C為單位圓上的動點,線段AC交線段OB于點M(點M異于點O、B),記△AOB的面積為S.0<θ<π2
22.如圖,A,B是單位圓上的相異兩定點(O為圓心),∠AOB=θ(),點C為單位圓上的動點,線段AC交線段OB于點M(點M異于點O、B),記△AOB的面積為S.0<θ<π2
(1)記f(θ)=2S+?OA,求f(θ)的表達式;AB
(2)若θ=60°
①求?CA的取值范圍;CB
②設=tOM(0<t<1),記OB=g(t),求g(t)的最小值.|AM||AC|組卷:105引用:6難度:0.4


