2023年陜西省西安市秦漢中學(xué)中考數(shù)學(xué)二模試卷

一、選擇題（共8小題，每小題3分，計(jì)24分每小題只有--一個(gè)選項(xiàng)是符合題目要求的）

• 1．計(jì)算（-2023）⁰=（　　）

  A．0

  B．1

  C．-1

  D．-2023
  組卷：639引用：11難度：0.8

  解析

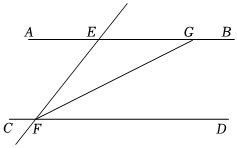• 2．如圖，AB∥CD，∠FGB=158°，F(xiàn)G平分∠EFD，則∠AEF的度數(shù)是（　　）

  A．42°

  B．44°

  C．48°

  D．52°
  組卷：356引用：2難度：0.7

  解析

• 3．計(jì)算：x³y⁵÷（xy）³=（　　）

  A．y

  B．x2y2

  C．y2

  D．x6y8
  組卷：246引用：4難度：0.8

  解析

• 4．下列條件中，能判定?ABCD為菱形的是（　　）

  A．AB=AD

  B．AC=BD

  C．AB=CD

  D．∠ABC=90°
  組卷：259引用：1難度：0.5

  解析

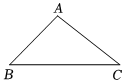• 5．如圖，在△ABC中，∠B=45°，tanC=

  2

  3

  ，AB=4

  2

  ，則△ABC的面積是（　　）

  A．12

  B．16

  C．12 2

  D．20
  組卷：187引用：1難度：0.4

  解析

• 6．若一次函數(shù)y=（a-2）x-b的圖象中y值隨x值的增大而增大，則a的值可以是（　　）

  A．4

  B．2

  C．-2

  D．-6
  組卷：869引用：5難度：0.7

  解析

• 7．如圖，AB，AD是⊙O的弦，點(diǎn)C在弦AB上，連接CO并延長(zhǎng)交⊙O于點(diǎn)D，已知∠CBO=32°，∠BAD=66°，則∠ADC的度數(shù)是（　　）

  A．28°

  B．32°

  C．34°

  D．38°
  組卷：186引用：3難度：0.6

  解析

• 8．二次函數(shù)y=ax²+bx+c的自變量x與函數(shù)值y的部分對(duì)應(yīng)值如下表：
  

  x	…	-2	-1	0	2	4	5	…
  y	…	-7	-2	1	1	-7	-14	…

  下列說法正確的是（　　）

  A．拋物線的開口向上

  B．當(dāng)x＞1時(shí)，y隨x的增大而增大

  C．二次函數(shù)的最大值是2

  D．拋物線與x軸只有一個(gè)交點(diǎn)
  組卷：196引用：3難度：0.7

  解析

三、解答題（共13小題，計(jì)81分解答應(yīng)寫出過程）

• 25．初三的學(xué)生麗麗和蘭蘭一起去大棚摘草莓，她們看到草莓棚其橫截面頂部為拋物線型，商家告訴她們大棚的一端固定在離地面高1m的墻體A處，另一端固定在離地面高2m的墻體B處，現(xiàn)對(duì)其橫截面建立如圖所示的平面直角坐標(biāo)系．已知大棚上某處離地面的高度y（m）與其離墻體A的水平距離x（m）之間的關(guān)系滿足y=-

  1

  2

  x²+mx+n,現(xiàn)測(cè)得A，B兩墻體之間的水平距離為4m.
  （1）求該拋物線的函數(shù)表達(dá)式；
  （2）麗麗的身高是1.65m,若她在草莓大棚中直立，當(dāng)她的頭頂剛好觸碰到大棚時(shí)，求她與墻體A之間的距離．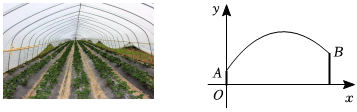
  
  組卷：332引用：1難度：0.5

  解析

• 26．[問題提出]
  （1）如圖①，在等腰直角△ABC中，∠B=90°，△ACD為等邊三角形，AD=4，則線段BD的長(zhǎng)為

  ．
  [問題解決]
  （2）如圖②，在等腰直角△ABC中，∠B=90°，BC=AB=2，以AC為直徑作半圓O，點(diǎn)D為

  ?

  AC

  上一動(dòng)點(diǎn)，求點(diǎn)B、D之間的最大距離；
  [問題探究]
  （3）一次手工制作課程中，老師要求小明和小麗組制作一種特殊的部件，部件的要求如圖③，部件是由直角△ABC以及弓形BDC組成，其中∠B=90°，AB=4，BC=6.4，DE=2.4，點(diǎn)E為BC的中點(diǎn)，DE⊥BC，這時(shí)候小明和小麗在討論這個(gè)部件，其中小麗說點(diǎn)A到

  ?

  BC

  的最大距離是點(diǎn)A、D之間的距離，小明說不對(duì)，你認(rèn)為誰(shuí)的說法正確？請(qǐng)說明理由，并求出點(diǎn)A到

  ?

  BC

  的最大距離．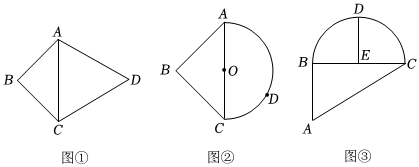
  
  組卷：327引用：1難度：0.3

  解析