2020-2021學年重慶一中高三（上）8月定時練習數學試卷

一、單項選擇題：在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知集合A={x|-1≤x≤2}，集合B={x|x＞2}，則A∩（?_RB）=（　　）

  A．（0，2]

  B．（0，2）

  C．[-1，2]

  D．（-1，2]
  組卷：56引用：2難度：0.8

  解析

• 2．函數f（x）=e^x+x-2的零點所在區間是（　　）

  A．（0，1）

  B．（1，2）

  C．（2，3）

  D．（3，4）
  組卷：70引用：14難度：0.9

  解析

• 3．函數

  f

  （

  x

  ）

  =

  2

  x

  2

  +

  2

  x

  +

  2

  的值域為（　　）

  A．（-∞，2]

  B．[2，+∞）

  C．（0，2]

  D．[1，2]
  組卷：2407引用：4難度：0.9

  解析

• 4．若方程-x²+ax+4=0的兩實根中一個小于-1，另一個大于2，則a的取值范圍是（　　）

  A．（0，3）	B．[0，3]
  C．（-3，0）	D．（-∞，0）∪（3，+∞）
  組卷：783引用：2難度：0.7

  解析

• 5．函數f（x）=

  1

  x

  -

  lnx

  -

  1

  的圖象大致是（　　）

  A．

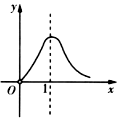
  B．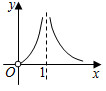

  C．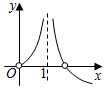

  D．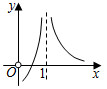
  組卷：324引用：24難度：0.9

  解析

• 6．2019年10月20日，第六屆世界互聯網大會發布了15項“世界互聯網領先科技成果”，其中有5項成果均屬于芯片領域，分別為華為高性能服務器芯片“鯤鵬920”、清華大學“面向通用人工智能的異構融合天機芯片”、“特斯拉全自動駕駛芯片”、寒武紀云端AI芯片、“思元270”、賽靈思“Versal自適應計算加速平臺”．現有3名學生從這15項“世界互聯網領先科技成果”中分別任選1項進行了解，且學生之間的選擇互不影響，則至少有1名學生選擇“芯片領域”的概率為（　　）

  A． 89 91

  B． 2 91

  C． 98 125

  D． 19 27
  組卷：175引用：6難度：0.8

  解析

• 7．已知a＞0，b＞0，且a+b=1，則

  ab

  4

  a

  +

  9

  b

  的最大值為（　　）

  A． 1 24

  B． 1 25

  C． 1 26

  D． 1 27
  組卷：401引用：6難度：0.7

  解析

四、解答題：解答應寫出文字說明、證明過程或演算步驟．

• 21．為了治療某種疾病，某科研機構研制了甲、乙兩種新藥，為此進行白鼠試驗．方案如下：每一輪選取兩只白鼠對藥效進行對比試驗．對于兩只白鼠，隨機選一只施以甲藥，另一只施以乙藥．一輪的治療結果得出后，再安排下一輪試驗.4輪試驗后，就停止試驗．甲、乙兩種藥的治愈率分別是

  2

  5

  和

  β

  （

  β

  ∈

  [

  3

  5

  ，

  4

  5

  ]

  ）

  ．
  （1）若β=

  3

  5

  ，求2輪試驗后乙藥治愈的白鼠比甲藥治愈的白鼠多1只的概率；
  （2）已知A公司打算投資甲、乙這兩種新藥的試驗耗材費用，甲藥和乙藥一次試驗耗材花費分別為3千元和（10β-1）千元，每輪試驗若甲、乙兩種藥都治愈或都沒有治愈，則該科研機構和A公司各承擔該輪試驗耗材總費用的50%．若甲藥治愈，乙藥未治愈，則A公司承擔該輪試驗耗材總費用的75%，其余由科研機構承擔．若甲藥未治愈，乙藥治愈，則A公司承擔該輪試驗耗材總費用的25%，其余由科研機構承擔．以A公司每輪支付試驗耗材費用的期望為標準，求A公司4輪試驗結束后支付試驗耗材最少費用為多少元？
  組卷：260引用：3難度：0.5

  解析

• 22．已知函數f（x）=x²+lnx-ax.
  （1）求函數f（x）的單調區間；
  （2）若f（x）≤2x²，對x∈[0，+∞）恒成立，求實數a的取值范圍；
  （3）當a=1時

  ，

  設

  g

  （

  x

  ）

  =

  x

  e

  x

  2

  -

  f

  （

  x

  ）

  -

  x

  -

  1

  ．若正實數λ₁，λ₂滿足λ₁+λ₂=1，x₁，x₂∈（0，+∞）（x₁≠x₂），證明：g（λ₁x₁+λ₂x₂）＜λ₁g（x₁）+λ₂g（x₂）．
  組卷：378引用：2難度：0.1

  解析