2020-2021學年北京人大附中九年級(下)限時練習數學試卷(9)
發布:2024/4/20 14:35:0
一、選擇題(本題共16分,每小題2分)第1-8題均有四個選項,符合題意的選項只有一個。
-
1.下列安全圖標中,是中心對稱圖形但不是軸對稱圖形的是( )
A. 
B. 
C. 
D.  組卷:226引用:6難度:0.9
組卷:226引用:6難度:0.9 -
2.經文旅部數據中心測算,2021年“五一”假期,北京市旅游總收入9300000000元,比2020年增長1.2倍,恢復到2019年的86%.將9300000000用科學記數法表示應為( )
A.93×108 B.9.3×109 C.0.93×1010 D.9.3×1010 組卷:210引用:1難度:0.8 -
3.正六邊形的外角和是( )
A.720° B.540° C.360° D.180° 組卷:1263引用:23難度:0.8 -
4.如圖是某個幾何體的三視圖,該幾何體是( )
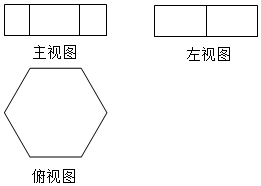
A.三棱柱 B.六棱錐 C.六棱柱 D.圓錐 組卷:268引用:1難度:0.6 -
5.如果m2-2m-2=0,那么代數式(m-
)?4m-4m的值是( )m22-mA.-2 B.-1 C.2 D.3 組卷:792引用:6難度:0.6 -
 6.實數a,b,c,d在數軸上的對應點的位置如圖所示.若b+d=0,則下列結論中正確的是( )
6.實數a,b,c,d在數軸上的對應點的位置如圖所示.若b+d=0,則下列結論中正確的是( )A.b+c>0 B. <1caC.ad>bc D.|a|<|d| 組卷:192引用:1難度:0.6 -
7.程老師制作了如圖1所示的學具,用來探究“邊邊角條件是否可確定三角形的形狀”問題.操作學具時,點Q在軌道槽AM上運動,點P既能在以A為圓心、以8為半徑的半圓軌道槽上運動,也能在軌道槽QN上運動.圖2是操作學具時,所對應某個位置的圖形的示意圖.

有以下結論:
①當∠PAQ=30°,PQ=6時,可得到形狀唯一確定的△PAQ;
②當∠PAQ=30°,PQ=9時,可得到形狀唯一確定的△PAQ;
③當∠PAQ=90°,PQ=10時,可得到形狀唯一確定的△PAQ;
④當∠PAQ=150°,PQ=12時,可得到形狀唯一確定的△PAQ.
其中所有正確結論的序號是( )A.②③ B.③④ C.②③④ D.①②③④ 組卷:1232引用:12難度:0.7 -
8.在對某種傳染性疾病進行流行病學調查的過程中,有專業機構提出:在一段時間沒有發生大規模群體感染的標志為“連續10天,每天新增疑似病例不超過7人”.根據過去10天里,甲、乙、丙、丁四地新增疑似病例數據,一定符合該標志的是( )
A.甲:總體平均數為3,中位數為4 B.乙:中位數為2,眾數為3 C.丙:總體平均數為1,總體方差大于0 D.丁:總體平均數為2,眾數為4 組卷:85引用:1難度:0.7
二、填空題(本題共16分,每小題2分)
-
9.寫一個大于2且小于3的無理數 .
組卷:348引用:12難度:0.9
三、解答題(本題共68分,第17-21題,每小題5分,第22題6分,第23題5分,第24-26題,每小題5分,第27、28題,每小題5分)
-
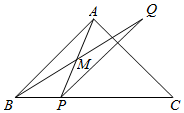 27.在△ABC中,∠BAC=90°,AB=AC,點P為射線BC上一動點(不與點B,C重合),以點P為中心,將線段PC逆時針旋轉α角(0°<α<180°),得到線段PQ,連接AP,BQ,M為線段BQ的中點.
27.在△ABC中,∠BAC=90°,AB=AC,點P為射線BC上一動點(不與點B,C重合),以點P為中心,將線段PC逆時針旋轉α角(0°<α<180°),得到線段PQ,連接AP,BQ,M為線段BQ的中點.
(1)如圖,當點P在線段BC上時,若M恰為AP的中點,求此時的值;BPPC
(2)寫出一個a的值,使得對于任意線段BC延長線上的點P,總有的值為定值,并證明.APPM組卷:140引用:2難度:0.5 -
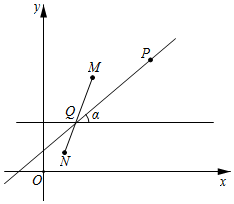 28.在平面直角坐標系xOy中,對于線段MN和點P.給出如下定義:若在線段MN上存在點Q,過點Q作y軸的垂線l,使得直線PQ與直線l所形成的角中,有一個角為α(0°<α≤90°),則稱點P是線段MN的“α-聯絡點”.特別地,當PQ與直線l重合時,記α=0°,此時點P是線段MN的“0°-聯絡點”.
28.在平面直角坐標系xOy中,對于線段MN和點P.給出如下定義:若在線段MN上存在點Q,過點Q作y軸的垂線l,使得直線PQ與直線l所形成的角中,有一個角為α(0°<α≤90°),則稱點P是線段MN的“α-聯絡點”.特別地,當PQ與直線l重合時,記α=0°,此時點P是線段MN的“0°-聯絡點”.
如圖是線段MN的一個“α-聯絡點”的示意圖.
已知點A(0,3),
(1)點B在直線x=3上,
①若點B的坐標為(3,-3),且它是線段OA的“α-聯絡點”,在α=30°和α=45°中,可能的α值為 .
②若點B既是線段OA的“45°-聯絡點”,又是線段OA的“60°-聯絡點”.寫出一個符合題意的點B的坐標;
(2)已知圖形G是邊長為a的等邊三角形,若圖形G上所有的點都是線段OA的“45°-聯絡點”,求a的最大值;
(3)⊙T的圓心為(t,0),直徑為1,點M,N在以A為圓心,2為半徑的圓上,且MN=2,若⊙T上所有的點都是線段MN的“45°-聯絡點”,直接寫出t的取值范圍.組卷:99引用:1難度:0.2


