2020-2021學年四川省涼山州西昌市北京外國語大學附屬西南外國語學校八年級（下）期中數學試卷

一、選擇題（共十題：共30分）

• 1．使式子

  x

  -

  2

  x＞2有意義的x的取值范圍是（　　）

  A．x≥2

  B．x＞2

  C．x=2

  D．x＜2
  組卷：3引用：1難度：0.9

  解析

• 2．下列各式中，最簡二次根式是（　　）

  A． 27

  B． 6

  C． 1 a

  D． 3 a 2
  組卷：302引用：12難度：0.9

  解析

• 3．下列計算正確的是（　　）

  A． 8 + 2 = 10

  B． 2 2 - 2 = 2

  C． 2 × 3 = 6

  D． 12 ÷ 2 = 6
  組卷：202引用：10難度：0.7

  解析

• 4．下列四組數分別表示三角形的三條邊長，其中能構成直角三角形的是（　　）

  A．2、3、4

  B．2、3、 7

  C． 2 、 3 、 5

  D．1、1、2
  組卷：194引用：8難度：0.9

  解析

• 5．直角三角形的兩邊長分別為6和8，則第三條邊長為（　　）

  A．10

  B．8

  C．6或8

  D． 2 7 或10
  組卷：20引用：2難度：0.7

  解析

• 6．下列條件中，能判定四邊形ABCD為平行四邊形的個數是（　　）
  ①AB∥CD，AD=BC；②AB=CD，AD=BC；③∠A=∠B，∠C=∠D；④AB=AD，CB=CD

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：983引用：4難度：0.5

  解析

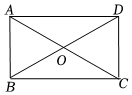• 7．如圖，矩形ABCD中，AB=3，兩條對角線AC，BD所夾的鈍角為120°，則對角線BD的長為（　　）

  A．3

  B．6

  C． 3 3

  D．10
  組卷：150引用：3難度：0.6

  解析

• 8．下列三個命題：①對頂角相等；②兩直線平行，內錯角相等；③相等的兩個實數的平方也相等．它們的逆命題成立的個數是（　　）

  A．0個

  B．1個

  C．2個

  D．3個
  組卷：79引用：4難度：0.7

  解析

三、解答題（共十題：共72分）

• 25．已知△ABC三條邊的長度分別是

  x

  +

  1

  ，

  （

  5

  -

  x

  ）

  2

  ，

  4

  -

  （

  4

  -

  x

  ）

  2

  ，記△ABC的周長為C_△ABC．
  （1）當x=2時，△ABC的最長邊的長度是

  （請直接寫出答案）；
  （2）請求出C_△ABC（用含x的代數式表示，結果要求化簡）；
  （3）我國南宋時期數學家秦九韶曾提出利用三角形的三邊長求面積的秦九韶公式：S=

  1

  4

  [

  a

  2

  b

  2

  -

  （

  a

  2

  +

  b

  2

  -

  c

  2

  2

  ）

  2

  ]

  ．其中三角形邊長分別為a,b,c,三角形的面積為S．
  若x為整數，當C_△ABC取得最大值時，請用秦九韶公式求出△ABC的面積．
  組卷：991引用：4難度：0.4

  解析

• 26．請解答下列各題：
  （1）根據兩點的坐標，構造直角三角形，求出兩直角邊的長，然后再求斜邊的長；
  

  兩點坐標	構造直角三角形	一直角邊長	另一直角邊長	斜邊長
  A（1，-2）B（4，2）	Rt△ABC	AC=4-1=3或AC=2-（-2）=4	BC=2-（-2）=4或BC=4-1=3	AB= （ 4 - 1 ） 2 + [ 2 - （ - 2 ） ] 2 =5
  M（-4，2）N（1，-3）	Rt△MPN			MN=

  （2）觀察表格中的關系，探究任意兩點坐標P₁（x₁，y₁），P（x₂，y₂）與點P₁，P₂之間的距離P₁P₂有什么關系？并證明你的結論．
  （3）求y=

  （

  x

  -

  1

  ）

  2

  +

  4

  +

  （

  x

  -

  4

  ）

  2

  +

  4

  的最小值．
  組卷：6引用：1難度：0.3

  解析