2023-2024學年浙江省杭州市蕭山區錢江片九年級（上）調研數學試卷（10月份）

一．選擇題（每小題3分，共30分）

• 1．下列各式中，不是二次函數的是（　　）

  A．y=-2x2	B．y=2（x-1）2+1
  C．y=（x-3）2-x2	D．y=a（8-a）
  組卷：89引用：3難度：0.7

  解析

• 2．下列事件中，是必然事件的是（　　）

  A．任意拋擲一枚硬幣，出現正面朝上

  B．從1、3、5、7、9這5張卡片中任抽一張是偶數

  C．投擲一枚普通骰子，朝上一面的點數是6

  D．從裝有一個黃球三個紅球的袋子中任取兩球，至少有一個是紅球
  組卷：132引用：6難度：0.8

  解析

• 3．二次函數y=x²的圖象向右平移3個單位，向下平移2個單位，得到新的圖象的函數表達式是（　　）

  A．y=（x+3）2+2

  B．y=（x-3）2+2

  C．y=（x+3）2-2

  D．y=（x-3）2-2
  組卷：235引用：9難度：0.7

  解析

• 4．五張完全相同的卡片上，分別畫有圓、平行四邊形、等腰三角形、矩形、正方形，現從中隨機抽取一張，恰好抽到既是軸對稱圖形，又是中心對稱圖形的概率是（　　）

  A． 1 5

  B． 3 5

  C． 4 5

  D．1
  組卷：299引用：4難度：0.5

  解析

• 5．如圖，在期末體育測試中，小朱擲出的實心球的飛行高度y（米）與水平距離x（米）之間的關系大致滿足二次函數

  y

  =

  -

  1

  10

  x

  2

  +

  3

  5

  x

  +

  8

  5

  ，則小朱本次投擲實心球的成績為（　　）

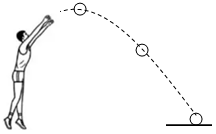
  A．7m

  B．7.5m

  C．8m

  D．8.5m
  組卷：1292引用：12難度：0.6

  解析

• 6．已知拋物線y=x²-2x+b的圖象上三個點的坐標分別為A（-1，y₁），B（2，y₂），C（4，y₃），則y₁，y₂，y₃的大小關系為（　　）

  A．y3＞y1＞y2

  B．y3＞y2＞y1

  C．y2＞y1＞y3

  D．y2＞y1＞y1
  組卷：123引用：4難度：0.5

  解析

• 7．已知二次函數y=（x-3）²-1，則當1≤x≤4時，該函數（　　）

  A．只有最大值3，無最小值

  B．有最大值3，有最小值0

  C．有最小值-1，有最大值3

  D．只有最小值-1，無最大值
  組卷：584引用：6難度：0.5

  解析

• 8．反比例函數

  y

  =

  k

  x

  （k≠0）圖象在二、四象限，則二次函數y=kx²-2x的大致圖象是（　　）

  A．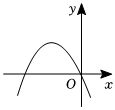

  B．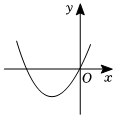

  C．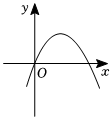

  D．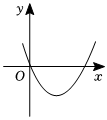
  組卷：827引用：9難度：0.9

  解析

三．解答題（本大題有8個小題，共66分.解答應寫出文字說明、證明過程或推演步驟.）

• 23．在平面直角坐標系中，設二次函數

  y

  =

  -

  1

  2

  （

  x

  -

  2

  m

  ）

  2

  +

  3

  -

  m

  （m是實數）．
  （1）當m=2時，判斷函數圖象與x軸有幾個交點；
  （2）小明說二次函數圖象的頂點在直線

  y

  =

  -

  1

  2

  x

  +

  3

  上，你認為他的說法對嗎？為什么？
  （3）已知點P（a+1，c），Q（4m-5+a,c）都在該二次函數圖象上，求證：

  c

  ≤

  13

  8

  ．
  組卷：529引用：5難度：0.5

  解析

• 24．如圖①，是一座拋物線型拱橋，小星學習二次函數后，受到該圖啟示設計了一建筑物造型，它的截面圖是拋物線的一部分（如圖②所示），拋物線的頂點在C處，對稱軸OC與水平線OA垂直，OC=9，點A在拋物線上，且點A到對稱軸的距離OA=3，點B在拋物線上，點B到對稱軸的距離是1．
  
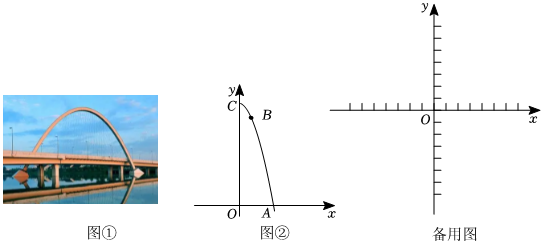
  （1）求拋物線的表達式；
  （2）如圖②，為更加穩固，小星想在OC上找一點P，加裝拉桿PA，PB，同時使拉桿的長度之和最短，請你幫小星找到點P的位置并求出坐標；
  （3）為了造型更加美觀，小星重新設計拋物線，其表達式為y=-x²+2bx+b-1（b＞0），當4≤x≤6時，函數y的值總大于等于9．求b的取值范圍．
  組卷：3425引用：15難度：0.3

  解析