當前位置：試卷中心 > 試卷詳情

2022-2023學年山東省日照市高一（下）期中數(shù)學試卷

發(fā)布：2024/6/13 8:0:9

一、單項選擇題：本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．若
sin
（
π
2
-
α
）
=
-
4
5
，則cos（π-α）的值為（　　）
A．
-
3
5
B．
-
4
5
C．
3
5
D．
4
5
組卷：359引用：1難度：0.7
解析
2．已知α角的終邊過點
（
sin
π
6
，-
sin
π
6
）
，則sinα的值為（　　）
A．
-
1
2
B．
1
2
C．
-
2
2
D．
2
2
組卷：273引用：2難度：0.8
解析
3．函數(shù)f（x）=xcosx的部分圖象大致為（　　）
A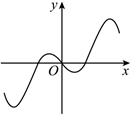． B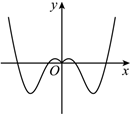． C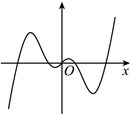． D．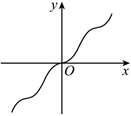
組卷：144引用：4難度：0.8
解析
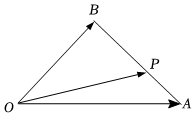4．如圖，在△OAB中，P為線段AB上的一點，且
BA
=
4
PA
．若
OP
=
x
OA
+
y
OB
，則（　　）
A．
x
=
3
4
，
y
=
1
4
B．
x
=
2
3
，
y
=
1
3
C．
x
=
1
3
，
y
=
2
3
D．
x
=
1
4
，
y
=
3
4
組卷：374引用：2難度：0.5
解析
5．將函數(shù)f（x）的圖像上所有的點向左平移
π
4
個單位長度，再把圖像上各點的橫坐標擴大到原來的2倍（縱坐標不變），得到函數(shù)
y
=
sin
（
x
2
+
5
π
12
）
的圖像，則f（x）=（　　）
A．
sin
（
2
x
-
π
3
）
B．
sin
（
x
+
π
6
）
C．
sin
（
2
x
+
π
6
）
D．
sin
（
x
-
π
6
）
組卷：106引用：2難度：0.8
解析

6．已知函數(shù)f（x）=sinx+cosx+|sinx-cosx|，下列結(jié)論正確的是（　　）

A．函數(shù)圖像關(guān)于

對稱

B．函數(shù)在

[

，

]

上單調(diào)遞增

C．若|f（x₁）|+|f（x₂）|=4，則

kπ

（

∈

）

D．函數(shù)f（x）的最小值為-2

組卷：209引用：5難度：0.6

解析

7．如圖等腰直角三角形OAB，OB=1，以AB為直徑作一半圓，點P為半圓上任意一點，則
OP
?
OB
的最大值是（　　）
A．1 B．
2
C．
3
D．
2
+
1
2
組卷：76引用：1難度：0.7
解析

當前模式為游客模式，立即登錄查看試卷全部內(nèi)容及下載

四、解答題：共70分。解答應寫出文字說明，證明過程或演算步驟。

21．如圖，角α的始邊與x軸的非負半軸重合，終邊與單位圓交于點A（x₁，y₁），將射線OA繞點O按逆時針方向旋轉(zhuǎn)
π
3
后與單位圓相交于點B（x₂，y₂），設(shè)f（α）=y₁+y₂．
（1）求
f
（
π
6
）
的值；
（2）若函數(shù)
g
（
x
）
=
f
（
2
x
-
π
3
）
，求g（x）的單調(diào)遞增區(qū)間；
（3）在（2）的條件下，函數(shù)
h
（
x
）
=
g
（
x
）
+
（
λ
-
1
）
f
（
x
-
π
2
）
的最小值為
-
2
3
，求實數(shù)λ的值．
組卷：66引用：3難度：0.6
解析
22．某小區(qū)地下車庫出入口通道轉(zhuǎn)彎處是直角拐彎雙車道，平面設(shè)計如圖所示，每條車道寬為3米．現(xiàn)有一輛汽車，車體的水平截面圖近似為矩形ABCD，它的寬AD為2米，車體里側(cè)CD所在直線與雙車道的分界線相交于E、F，記∠DAE=θ．
（1）若汽車在轉(zhuǎn)彎的某一刻，A，B都在雙車道的分界線上，直線CD恰好過路口邊界O，且
θ
=
π
6
，求此汽車的車長AB；
（2）為保證行車安全，在里側(cè)車道轉(zhuǎn)彎時，車體不能越過雙車道分界線，求汽車車長AB的最大值；
（3）某研究性學習小組記錄了里側(cè)車道的平均道路通行密度（輛/km），統(tǒng)計如下：

時間 7：00 7：15 7：30 7：45 8：00

里側(cè)車道通行密度 110 130 110 90 110

現(xiàn)給出兩種函數(shù)模型：
①f（x）=Asinωx+B（A＞0，ω＞0，B＞0）；
②g（x）=a|x-b|+c（a,b,c∈R），
請你根據(jù)上表中的數(shù)據(jù)，從①②中選擇最合適的函數(shù)模型來描述里側(cè)車道早七點至八點的平均道路通行密度（單位：輛/km）與時間x（單位：分）的關(guān)系（其中x為7：00至8：00所經(jīng)過的時間，例如7：30即x=30分），并根據(jù)表中數(shù)據(jù)求出相應函數(shù)的解析式．
組卷：25引用：1難度：0.5
解析