2023-2024學年江蘇省蘇州市部分學校高三（上）期中數學試卷

一、選擇題（共8小題，每小題5分，共40分）

• 1．集合A={-1，0，1}，B={y|y=sinx,x∈R}，則（　　）

  A．A∩B=B

  B．A∪B=B

  C．A=B

  D．?RA=B
  組卷：75引用：5難度：0.8

  解析

• 2．復數z=

  1

  1

  +

  i

  （i是虛數單位）的共軛復數在復平面上對應的點位于第（　　）象限．

  A．一

  B．二

  C．三

  D．四
  組卷：60引用：4難度：0.9

  解析

• 3．若cos（

  π

  4

  -α）=

  3

  5

  ，則sin2α=（　　）

  A． 7 25

  B． 1 5

  C．- 1 5

  D．- 7 25
  組卷：12479引用：109難度：0.7

  解析

• 4．利用誘導公式可以將任意角的三角函數值轉化為0°～90°之間角的三角函數值，而這個范圍內的三角函數值又可以通過查三角函數表得到．如表為部分銳角的正弦值，則tan1600°的值為（　　）（小數點后保留2位有效數字）
  

  α	10°	20°	30°	40°	50°	60°	70°	80°
  sinα	0.1736	0.3420	0.5000	0.6427	0.7660	0.8660	0.9397	0.9848

  A．-0.42

  B．-0.36

  C．0.36

  D．0.42
  組卷：158引用：3難度：0.8

  解析

• 5．定義在區間

  （

  0

  ，

  π

  2

  ）

  上的函數y=3cosx與y=8tanx的圖象交點為P（x₀，y₀），則sinx₀的值為（　　）

  A． 1 3

  B． 3 3

  C． 2 3

  D． 2 2 3
  組卷：129引用：3難度：0.8

  解析

• 6．已知

  OA

  ，

  OB

  ，

  OC

  均為單位向量，且滿足

  1

  2

  OA

  +

  OB

  +

  OC

  =

  0

  ，則

  AB

  ?

  AC

  的值為（　　）

  A． 3 8

  B． 5 8

  C． 7 8

  D． 19 8
  組卷：389引用：6難度：0.7

  解析

• 7．已知函數f（x）的定義域為R，且f（x+2）=2-f（x），f（2-3x）為偶函數，若f（0）=0，

  n

  ∑

  k

  =

  1

  f

  （

  k

  ）

  =

  123

  ，則n的值為（　　）

  A．117

  B．118

  C．122

  D．123
  組卷：148引用：2難度：0.6

  解析

四、解答題（共6小題，共70分）

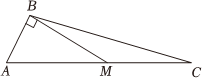• 21．△ABC中，內角A，B，C所對的邊分別為a,b,c,

  a

  =

  3

  2

  ，

  bsin

  B

  +

  C

  2

  =

  5

  2

  asin

  B

  ．
  （1）求sinA；
  （2）如圖，點M為邊AC上一點，

  MB

  =

  MC

  ，

  ∠

  ABM

  =

  π

  2

  ，求△ABC的面積．
  組卷：112引用：2難度：0.5

  解析

• 22．已知二次函數y=f（x）的圖象與直線y=-6只有一個交點，滿足f（0）=-2，且函數f（x-2）是偶函數，

  g

  （

  x

  ）

  =

  f

  （

  x

  ）

  x

  ．
  （1）求二次函數y=f（x）的解析式；
  （2）若對任意x∈[1，2]，t∈[-4，4]，g（x）≥-m²+tm恒成立，求實數m的范圍；
  （3）若函數

  y

  =

  g

  （

  |

  x

  |

  +

  3

  ）

  +

  k

  ?

  2

  |

  x

  |

  +

  3

  -

  11

  恰好三個零點，求k的值及該函數的零點．
  組卷：119引用：4難度：0.6

  解析