2023年福建省三明市寧化縣中考數學適應性試卷
發布：2024/7/13 8:0:9
一、選擇題：本題共10小題，每小題4分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.
-
1．-6的絕對值是（ ）
組卷：487引用：63難度：0.9 -
2．如圖是一個幾何體的三視圖，則該幾何體的展開圖可以是（ ）組卷：1141引用：76難度：0.7 -
3．某種玫瑰花花粉的直徑約為0.0000028m,將數據0.0000028用科學記數法表示為（ ）
組卷：31引用：3難度：0.8 -
4．下列整式的計算正確的是（ ）
組卷：150引用：4難度：0.5 -
5．如圖，已知一組平行線a∥b∥c,被直線m、n所截，交點分別為A、B、C和D、E、F，且AB=3，BC=4，EF=4.8，則DE=（ ）組卷：1488引用：9難度：0.7 -
6．為了解某校學生的身高情況，隨機抽取該校男生、女生進行抽樣調查．已知抽取的樣本中，男生、女生的人數相同，利用所得數據繪制如下統計圖表：
身高情況分組表（單位：cm）：組別 A B C D E 身高 x＜155 155≤x＜160 160≤x＜165 165≤x＜170 x≥170 
根據圖表提供的信息，樣本中，身高在160≤x＜170之間的女生人數為（ ）組卷：146引用：2難度：0.9 -
7．在我國古代數學名著《算法統宗》里有一道“蕩秋千”的問題：“平地秋千未起，踏板一尺離地．送行二步與人齊，五尺人高曾記．仕女佳人爭蹴，終朝笑語歡嬉．良工高士素好奇，算出索長有幾？”譯文：“有一架秋千，當它靜止時，踏板離地1尺，將它往前推送10尺（水平距離）時，秋千的踏板就和身高為5尺的人一樣高，秋千的繩索始終是拉直的，試問繩索有多長？”設繩索長為x尺，則所列方程為（ ）組卷：516引用：18難度：0.6 -
8．閱讀理解：為計算tan15°三角函數值，我們可以構建Rt△ACB（如圖），使得∠C=90°，∠ABC=30°，延長CB使BD=AB，連接AD，可得到∠D=15°，所以tan15°==ACCD=12+3=2-2-3（2+3）（2-3）．類比這種方法，請你計算tan22.5°的值為（ ）3組卷：1783引用：8難度：0.6
三、解答題：本題共9小題，共86分.解答應寫出文字說明、證明過程或演算步驟.
-
24．[初步嘗試]
（1）如圖①，在三角形紙片ABC中，∠ACB=90°，將△ABC折疊，使點B與點C重合，折痕為MN，則AM與BM的數量關系為 ；
[思考說理]
（2）如圖②，在三角形紙片ABC中，AC=BC=6，AB=10，將△ABC折疊，使點B與點C重合，折痕為MN，求的值；AMBM
[拓展延伸]
（3）如圖③，在三角形紙片ABC中，AB=9，BC=6，∠ACB=2∠A，將△ABC沿過頂點C的直線折疊，使點B落在邊AC上的點B′處，折痕為CM．
①求線段AC的長；
②若點O是邊AC的中點，點P為線段OB′上的一個動點，將△APM沿PM折疊得到△A′PM，點A的對應點為點A′，A′M與CP交于點F，求的取值范圍．PFMF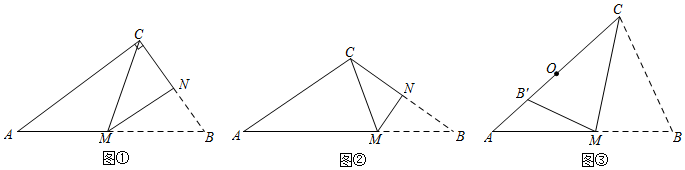
組卷：5162引用：16難度：0.1 -
25．已知二次函數L1：y1=x2+6x+5k和L2：y2=kx2+6kx+5k,其中k≠0．
（1）寫出兩條有關二次函數L1和L2共有的性質或結論；
（2）若兩條拋物線L1和L2相交于點E，F，當k的值發生變化時，判斷線段EF的長度是否發生變化，并說明理由；
（3）在（2）中，若二次函數L1的頂點為M，二次函數L2的頂點為N；
①當k為何值時，點M與點N關于直線EF對稱？
②是否存在實數k,使得MN=2EF？若存在，求出實數k的值；若不存在，請說明理由．組卷：96引用：1難度：0.4