當前位置：試卷中心 > 試卷詳情

2022-2023學年廣東省深圳市高一（上）期末數學試卷

發布：2024/12/19 2:30:2

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知集合A={3，5，7，8}，B={2，3，4，5，7}，則A∩B=（　　）
A．{8} B．{2，3，4，5，7，8}
C．{2，4，8} D．{3，5，7}
組卷：86引用：2難度：0.9
解析
2．命題p：?x∈[0，π]，sinxcosx≥0，則?p為（　　）
A．?x?[0，π]，sinxcosx＜0 B．?x∈[0，π]，sinxcosx≤0
C．?x∈[0，π]，sinxcosx≥0 D．?x∈[0，π]，sinxcosx＜0
組卷：93引用：2難度：0.7
解析
3．已知
tanα
=
1
2
，則
2
cosα
-
sinα
cosα
=（　　）
A．1 B．
3
2
C．
-
3
2
D．
-
2
3
組卷：615引用：3難度：0.7
解析
4．蕩秋千是中華大地上很多民族共有的游藝競技項目．據現有文獻記載，它源自先秦．位于廣東清遠的天子山懸崖秋千建在高198米的懸崖邊上，該秋千的纜索長8米，蕩起來最大擺角為170°，則該秋千最大擺角所對的弧長為（　　）
A．
68
π
9
米 B．
34
π
9
米 C．13.6米 D．198米
組卷：174引用：3難度：0.7
解析
5．設f（x）=
f
（
f
（
x
+
5
）
）
，
x
＜
10
2
x
-
15
，
x
≥
10
，則f（9）的值為（　　）
A．9 B．11 C．28 D．14
組卷：203引用：12難度：0.8
解析
6．已知函數f（x）=lg（2cosx-1），則函數f（x）的定義域為（　　）
A．
（
2
kπ
-
π
3
，
2
kπ
+
π
3
）
，
k
∈
Z
B．
[
2
kπ
-
π
3
，
2
kπ
+
π
3
]
，
k
∈
Z
C．
（
2
kπ
-
π
6
，
2
kπ
+
π
6
）
，
k
∈
Z
D．
[
2
kπ
-
π
6
，
2
kπ
+
π
6
]
，
k
∈
Z
組卷：373引用：3難度：0.7
解析
7．已知
α
∈
（
0
，
π
）
，
cosα
=
5
5
，則
cos
（
α
-
π
）
[
2
sin
（
α
+
π
）
+
sin
（
α
+
π
2
）
]
+
co
s
2
（
α
+
3
π
2
）
=（　　）
A．
4
5
B．
7
5
C．
8
5
D．
9
5
組卷：270引用：3難度：0.8
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

21．已知f（x）為R上的奇函數，g（x）為R上的偶函數，且
f
（
x
）
+
g
（
x
）
=
1
2
x
．
（1）判斷函數f（x）的單調性，并證明；
（2）若關于x的不等式
2
g
（
x
）
+
a
2
x
-
1
-
a
≥
0
在（0，+∞）上恒成立，求實數a的取值范圍．
組卷：232引用：3難度：0.5
解析
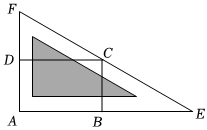22．如圖，有一個小矩形公園ABCD，其中AB=20m,AD=10m,現過點C修建一條筆直的圍墻（不計寬度）與AB和AD的延長線分別交于點E，F，現將小矩形公園擴建為三角形公園AEF．
（1）當AE多長時，才能使擴建后的公園△AEF的面積最小？并求出△AEF的最小面積．
（2）當擴建后的公園△AEF的面積最小時，要對其進行規劃，要求中間為三角形綠地（圖中陰影部分），周圍是等寬的公園健步道，如圖所示．若要保證綠地面積不小于總面積的
3
4
，求健步道寬度的最大值．（小數點后保留三位小數）
參考數據：
3
≈
1
.
732
，
5
≈
2
.
236
，
15
≈
3
.
873
．
參考公式：
tan
2
θ
=
2
tanθ
1
-
ta
n
2
θ
．
組卷：140引用：1難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．{8}	B．{2，3，4，5，7，8}
C．{2，4，8}	D．{3，5，7}

A．?x?[0，π]，sinxcosx＜0	B．?x∈[0，π]，sinxcosx≤0
C．?x∈[0，π]，sinxcosx≥0	D．?x∈[0，π]，sinxcosx＜0

A．（ 2 kπ - π 3 ， 2 kπ + π 3 ）， k ∈ Z	B． [ 2 kπ - π 3 ， 2 kπ + π 3 ] ， k ∈ Z
C．（ 2 kπ - π 6 ， 2 kπ + π 6 ）， k ∈ Z	D． [ 2 kπ - π 6 ， 2 kπ + π 6 ] ， k ∈ Z

2022-2023學年廣東省深圳市高一（上）期末數學試卷

一、選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．已知集合A={3，5，7，8}，B={2，3，4，5，7}，則A∩B=（ ）

2．命題p：?x∈[0，π]，sinxcosx≥0，則?p為（ ）

3．已知tanα=12，則2cosα-sinαcosα=（ ）

4．蕩秋千是中華大地上很多民族共有的游藝競技項目．據現有文獻記載，它源自先秦．位于廣東清遠的天子山懸崖秋千建在高198米的懸崖邊上，該秋千的纜索長8米，蕩起來最大擺角為170°，則該秋千最大擺角所對的弧長為（ ）

5．設f（x）=f（f（x+5）），x＜102x-15，x≥10，則f（9）的值為（ ）

6．已知函數f（x）=lg（2cosx-1），則函數f（x）的定義域為（ ）

7．已知α∈（0，π），cosα=55，則cos（α-π）[2sin（α+π）+sin（α+π2）]+cos2（α+3π2）=（ ）

四、解答題：本題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

21．已知f（x）為R上的奇函數，g（x）為R上的偶函數，且f（x）+g（x）=12x．（1）判斷函數f（x）的單調性，并證明；（2）若關于x的不等式2g（x）+a2x-1-a≥0在（0，+∞）上恒成立，求實數a的取值范圍．

1．已知集合A={3，5，7，8}，B={2，3，4，5，7}，則A∩B=（　　）

2．命題p：?x∈[0，π]，sinxcosx≥0，則?p為（　　）

3．已知
tanα
=
1
2
，則
2
cosα
-
sinα
cosα
=（　　）

5．設f（x）=
f
（
f
（
x
+
5
）
）
，
x
＜
10
2
x
-
15
，
x
≥
10
，則f（9）的值為（　　）

6．已知函數f（x）=lg（2cosx-1），則函數f（x）的定義域為（　　）

7．已知
α
∈
（
0
，
π
）
，
cosα
=
5
5
，則
cos
（
α
-
π
）
[
2
sin
（
α
+
π
）
+
sin
（
α
+
π
2
）
]
+
co
s
2
（
α
+
3
π
2
）
=（　　）

21．已知f（x）為R上的奇函數，g（x）為R上的偶函數，且
f
（
x
）
+
g
（
x
）
=
1
2
x
．
（1）判斷函數f（x）的單調性，并證明；
（2）若關于x的不等式
2
g
（
x
）
+
a
2
x
-
1
-
a
≥
0
在（0，+∞）上恒成立，求實數a的取值范圍．